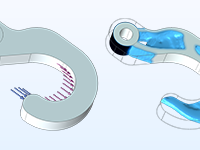
Ottimizzazione topologica strutturale
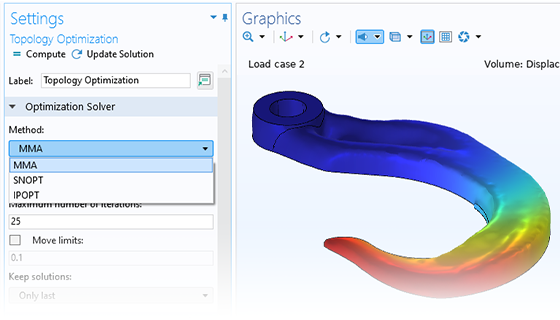
Ottimizzazione topologica di un gancio in cui il materiale è distribuito in modo ideale per un dato peso totale.
Optimization Module
Ottimizzare i modelli multifisici
L'Optimization Module, un add-on per COMSOL Multiphysics®, fornisce strumenti per l'ottimizzazione dei parametri, della forma e della topologia, nonché per la stima dei parametri. Può essere usato insieme ad altri moduli della suite di prodotti COMSOL per ottimizzare dispositivi e processi che coinvolgono fenomeni come l'elettromagnetismo, la meccanica strutturale, l'acustica, la fluidodinamica, il trasferimento di calore e altro. È possibile ottimizzare le dimensioni geometriche quando l'Optimization Module è combinato con il CAD Import Module, il Design Module o uno qualsiasi dei prodotti LiveLink™ per il CAD.
Iniziando con una funzione obiettivo da migliorare e un insieme di variabili di progetto da cambiare, insieme a un insieme opzionale di vincoli, il software cercherà un progetto ottimale. Qualsiasi input al modello - che siano dimensioni geometriche, forme dei pezzi, proprietà dei materiali o distribuzione dei materiali - può essere trattato come variabile di progetto, e qualsiasi risultato del modello può essere usato come funzione obiettivo, che viene poi minimizzata o massimizzata.
Contatta COMSOL
Cosa puoi ottimizzare con l'Optimization Module
L'Optimization Module può essere combinato con uno qualsiasi dei prodotti aggiuntivi COMSOL® per eseguire l'ottimizzazione in diverse aree fisiche.
Ottimizzazione di bobine
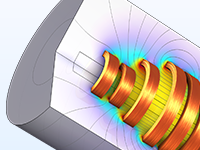
Ottimizzazione dei parametri e della forma di una bobina a dieci giri, ottimizzata rispetto alla densità di flusso magnetico e alla dissipazione di potenza.
Ottimizzazione dei parametri per i magneti
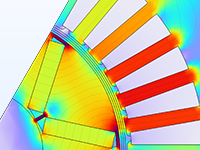
Ottimizzazione dei parametri di un motore elettrico per identificare la migliore posizione e forma dei magneti permanenti in base alla coppia.
Ottimizzazione della topologia per magneti
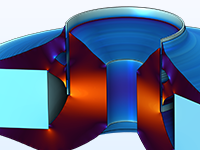
Ottimizzazione della topologia di un circuito magnetico utilizzato in un altoparlante per ridurre la risposta non lineare a grandi spostamenti.
Ottimizzazione dei componenti degli altoparlanti
L'ottimizzazione della forma della cupola del tweeter di un altoparlante e della guida d'onda permette di ottenere una curva di risposta più piatta e un migliore diagramma di radiazione.
Ottimizzazione della risposta in frequenza acustica
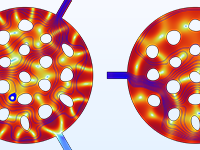
Ottimizzazione della forma di un demultiplexer acustico; l'energia acustica va a diverse porte di uscita per diverse bande di frequenza.
Ottimizzazione fluidodinamica
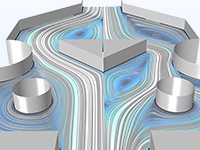
Ottimizzazione dei parametri, della forma e della topologia per una microvalvola Tesla che massimizza il rapporto della caduta di pressione per il flusso bidirezionale.
Ottimizzazione delle reti di condutture
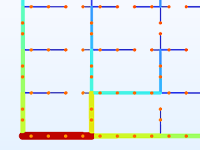
Ottimizzazione topologica del layout di una rete di teleriscaldamento.
Caratteristiche e funzionalità dell'Optimization Module
COMSOL Multiphysics® fornisce interfacce utente specializzate con solutori dedicati per i tipi di ottimizzazione disponibili.
Ottimizzazione dei parametri
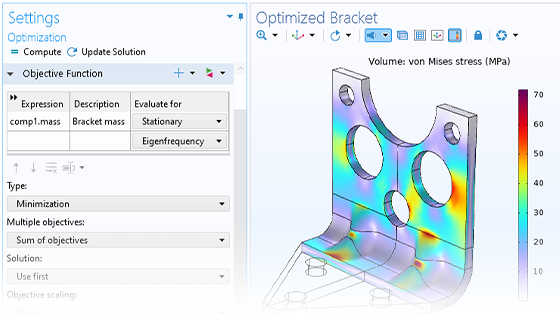
Per impostare un'ottimizzazione dei parametri in COMSOL Multiphysics®, è sufficiente aggiungere semplicemente uno studio generale Optimization. Una finestra di impostazioni associata richiede all'utente di aggiungere una funzione obiettivo, variabili e parametri di controllo e vincoli. I parametri usati per l'ottimizzazione dei parametri possono essere gli stessi che sono stati utilizzati per impostare il modello in primo luogo, come le dimensioni della geometria, le proprietà dei materiali o i carichi limite. Mentre uno sweep parametrico darà una panoramica dello spazio dei parametri di progettazione, un'ottimizzazione dei parametri restituirà i parametri ottimali e i valori della funzione obiettivo.
Quando si esegue un'ottimizzazione dei parametri con parametri che definiscono le dimensioni della geometria, il remeshing è necessario a ogni iterazione; questo processo è completamente automatico con l'Optimization Module. La soluzione ottimale è sempre una vera parte CAD che può essere immediatamente esportata nei formati CAD standard del settore. Questa funzionalità richiede il CAD Import Module, il Design Module o uno dei prodotti LiveLink™ per il CAD.
Ottimizzazione topologica
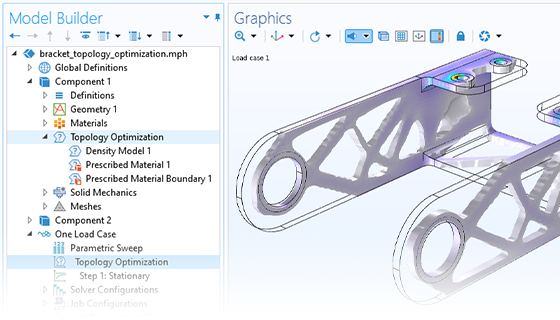
L'ottimizzazione topologica offre una libertà ancora maggiore nella variazione della geometria rispetto all'ottimizzazione dei parametri e della forma. Questo approccio permette la rimozione e l'aggiunta di materiale durante il processo di ottimizzazione, consentendo la creazione di fori nella geometria non presenti originariamente nel progetto. Questo metodo si traduce tipicamente in un design dall'aspetto organico, il che lo rende un metodo popolare per il light-weighting. Un'interfaccia utente e uno studio dedicati sono disponibili per l'ottimizzazione della topologia.
L'estrema libertà di progettazione associata all'ottimizzazione topologica può portare a progetti che non possono essere prodotti con i metodi convenzionali. È quindi comune introdurre vincoli di produzione, che consentono di produrre il progetto ottimizzato con l'estrusione o la fresatura.
Proprio come con l'ottimizzazione della forma, il remeshing non è richiesto per l'ottimizzazione topologica. Il progetto ottimale e semplificato è reso disponibile nei formati STL, 3MF o PLY per un ulteriore uso in un altro software o per l'analisi di verifica all'interno di COMSOL Multiphysics®.
Solutori basati sul gradiente
I metodi di ottimizzazione basati sul gradiente sono usati quando le derivate possono essere calcolate in modo efficiente usando il metodo adiacente. Questo è possibile per obiettivi o vincoli personalizzati, purché questi siano differenziabili. Questo è possibile grazie alla differenziazione simbolica presente nella tecnologia di base di COMSOL Multiphysics®, che fornisce la flessibilità necessaria per risolvere problemi multifisici personalizzati.
L'ottimizzazione basata sul gradiente può essere usata quando un problema di progettazione prevedere migliaia, o anche milioni, di variabili. Questo è spesso il caso dell'ottimizzazione della forma o della topologia, dove le variabili di progetto rappresentano quantità di campo che sono distribuite nello spazio e rappresentate da valori diversi in ogni elemento della mesh.
I metodi basati sul gradiente calcolano simultaneamente tutte le derivate analitiche, mentre i metodi senza derivate devono approssimare ogni derivata e richiedono quindi più tempo all'aumentare del numero di variabili di progetto.
I metodi basati sul gradiente inclusi nell'Optimization Module sono:
- Metodo degli asintoti mobili (sia MMA che GCMMA)
- Ottimizzatore del punto interno (IPOPT)
- Ottimizzatore sparsa non lineare (SNOPT)
- Levenberg-Marquardt
Sono supportati per i seguenti tipi di studio:
- Stationary, including:
- Frequency Domain
- Frequency-Stationary
- Eigenvalue:
- Eigenfrequency
- Stationary Then Eigenfrequency
- Time-dependent and Frequency-Transient:
- Fully discrete adjoint
- Semidiscrete adjoint
Ottimizzazione di forma
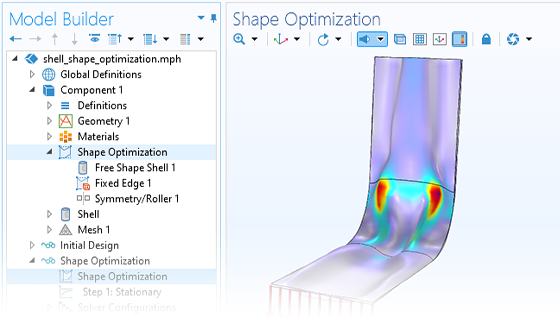
Come alternativa alla variazione di un insieme di parametri CAD, si possono utilizzare le funzionalità predefinite per l'ottimizzazione di forma in modo da permettere alla geometria di deformarsi più o meno liberamente. Questo approccio permette una maggiore libertà e a volte può produrre anche risultati migliori rispetto all'ottimizzazione dei parametri. È disponibile una serie di interfacce utente dedicate per definire facilmente le deformazioni dei contonri permesse in un modello 2D o 3D. Inoltre, è disponibile una funzione specializzata per l'ottimizzazione di forma di shell, così come un tipo di studio di ottimizzazione di forma per il controllo dei solutori.
Gli strumenti utilizzati per l'ottimizzazione della forma nei solidi sono basati su metodi che deformano la mesh in modo controllato, dove non è richiesto il remeshing. La geometria ottimale è disponibile in un formato di mesh di superficie sfaccettata, come STL, 3MF o PLY. Questa geometria può poi essere riutilizzata in un'analisi separata all'interno di COMSOL Multiphysics® o esportata per l'uso in un altro software.
Stima dei parametri
Un modello è accurato solo quanto il suo input, ma può essere difficile ottenere parametri dei materiali accurati dai fornitori. Per tenere conto delle non linearità, potrebbe essere necessario eseguire degli esperimenti. Tuttavia, cercare di progettare esperimenti che permettano di estrarre i parametri desiderati con metodi analitici può essere impegnativo.
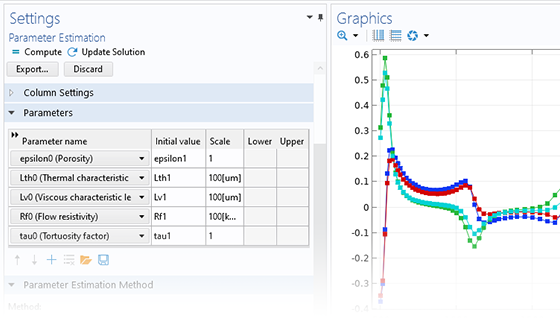
Una soluzione a questi problemi è quella di utilizzare la funzionalità di stima dei parametri dell'Optimization Module per trovare l'insieme dei parametri di un modello che minimizza la deviazione tra l'esperimento fisico e quello simulato. Oltre all'interfaccia per la stima generale dei parametri, è disponibile un'interfaccia utente specializzata per il fitting di una curva (rappresentata da un'espressione del modello) ai dati dipendenti dal tempo.
Il metodo di stima dei parametri si basa sull'adattamento ai minimi quadrati e può essere utilizzato quando i dati di riferimento sono una funzione del tempo o un singolo parametro. In molti casi, otterrete una stima della varianza e della confidenza dei parametri stimati.
Per i primi passi con la stima dei parametri, è disponibile un'app pronta all'uso. Gli utenti possono importare i dati di misurazione o utilizzare i campioni del tutorial incorporato, oppure inserire espressioni di modello personalizzate per la curva da adattare.
Solutori senza derivate
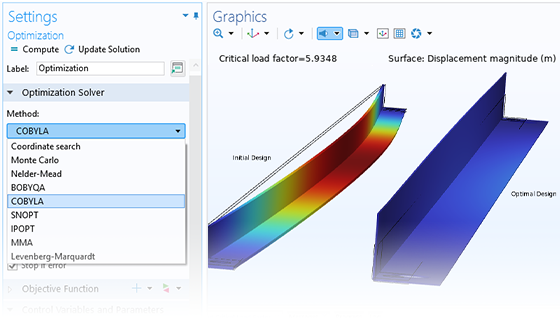
I metodi di ottimizzazione senza derivate si usano quando le direzioni di ricerca necessarie al solutore di ottimizzazione possono essere calcolate solo indirettamente. Questo è spesso il caso dell'ottimizzazione dei parametri dove le variabili di controllo rappresentano le dimensioni della geometria e il remeshing è necessario in ogni passo di iterazione.
I metodi senza derivate inclusi nell'Optimization Module sono:
- Nelder-Mead (il metodo Simplex)
- Ottimizzazione dei vincoli tramite approssimazione quadratica (BOBYQA)
- Ottimizzazione dei vincoli per approssimazione lineare (COBYLA)
- Ottimizzazione globale efficiente (EGO)
App di ottimizzazione e simulazione
L'uso dell'Application Builder insieme all'Optimization Module consente a un più ampio gruppo di utenti di eseguire studi di ottimizzazione in modo indipendente, senza la necessità di consultare un esperto di simulazione.
Per esempio, i modelli di ottimizzazione possono includere la stima dei parametri basata su dati sperimentali; un'app su misura per questo particolare compito permetterebbe all'utente di inserire vari set di dati sperimentali senza preoccuparsi dei dettagli del modello di ottimizzazione stesso.
L'uso delle app offre anche un flusso di lavoro più efficiente per il controllo ottimale. L'Optimization Module può essere usato per identificare quale input transitorio genera un output transitorio desiderato. In questi casi, potrebbe essere il caso di regolare l'output desiderato in base ai risultati sperimentali. Creare un'app per questo compito racchiude la complessità di questo processo in un'interfaccia utente personalizzata, permettendo a vari utenti di eseguire simulazioni di controllo ottimale semplicemente specificando gli output desiderati.
Ogni esigenza di business e di simulazione è diversa. Per valutare se il software COMSOL Multiphysics® soddisfa o meno le vostre esigenze, non dovete fare altro che contattarci. Parlando con uno dei nostri tecnici commerciali, riceverete consigli personalizzati ed esempi completamente documentati per aiutarvi a ottenere il massimo dalla vostra valutazione e guidarvi a scegliere l'opzione di licenza migliore per soddisfare le vostre esigenze.
Basta cliccare sul pulsante "Contatta COMSOL", inserire i propri contatti ed eventuali commenti o domande specifiche, e inviare la richiesta. Riceverete una risposta entro un giorno lavorativo.
Il prossimo passo?
Richiedi una dimostrazione del software