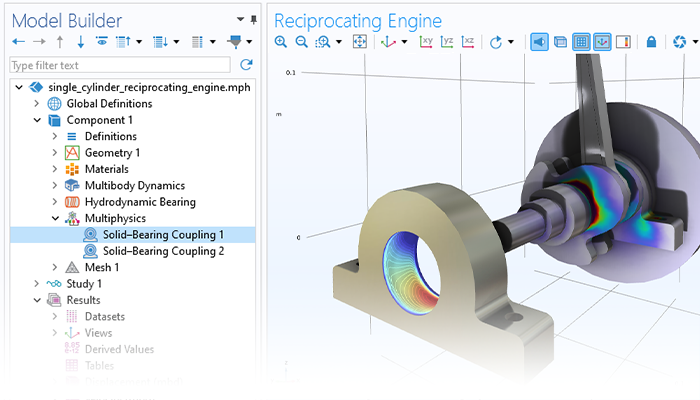
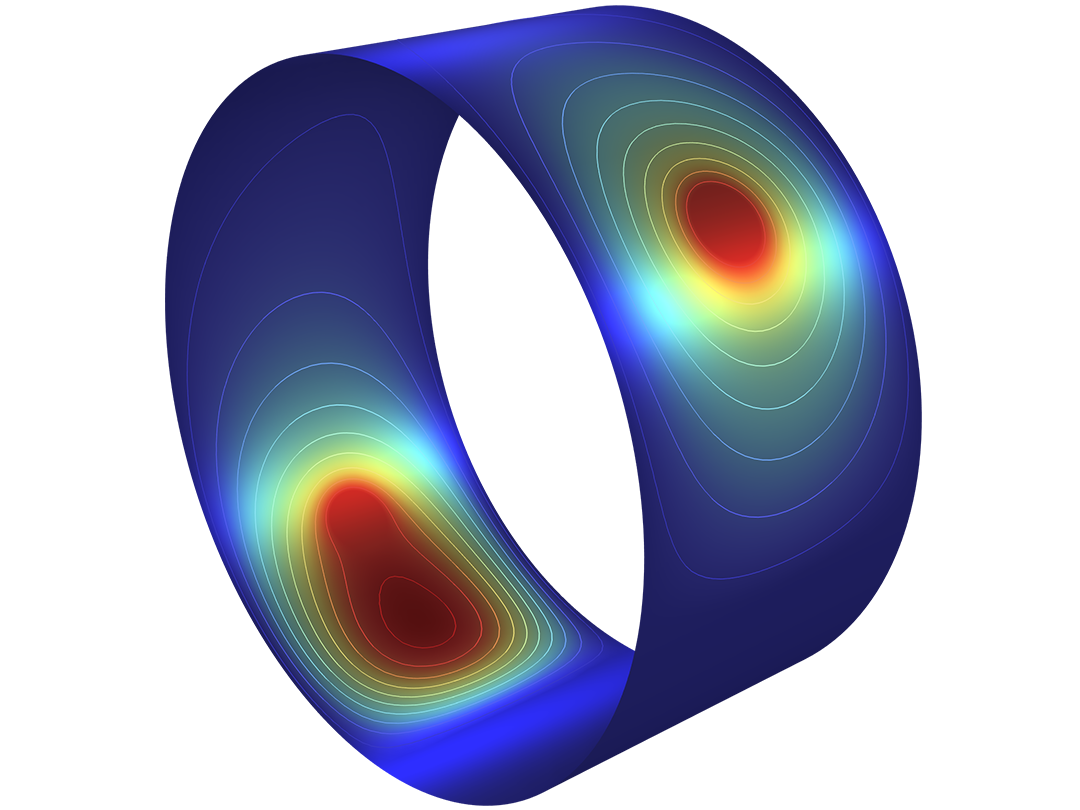Analizzare i sistemi rotore-cuscinetto
Il comportamento fisico delle macchine rotanti è fortemente influenzato dalle vibrazioni, che sono amplificate dalla rotazione e dalla forma delle macchine stesse. Anche i gruppi di rotori perfettamente simmetrici presentano una separazione dei modi con l'aumento della velocità di rotazione. Ciò implica che il comportamento abituale di modi identici in piani di simmetria perpendicolari non è applicabile agli alberi rotanti. Inoltre, anche piccole imperfezioni e squilibri possono dare origine ad ampiezze di vibrazione significative quando si opera vicino alle frequenze naturali del sistema rotante.
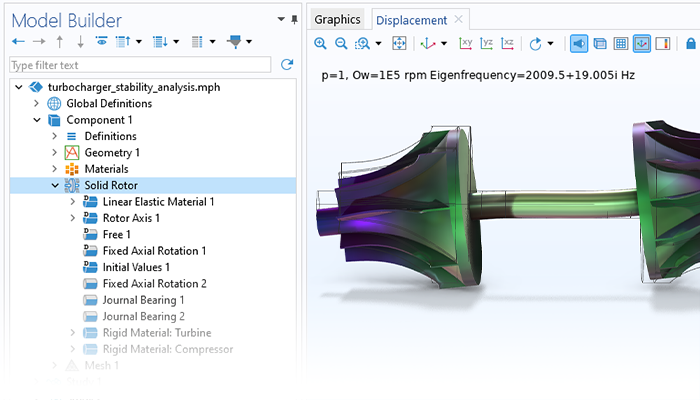
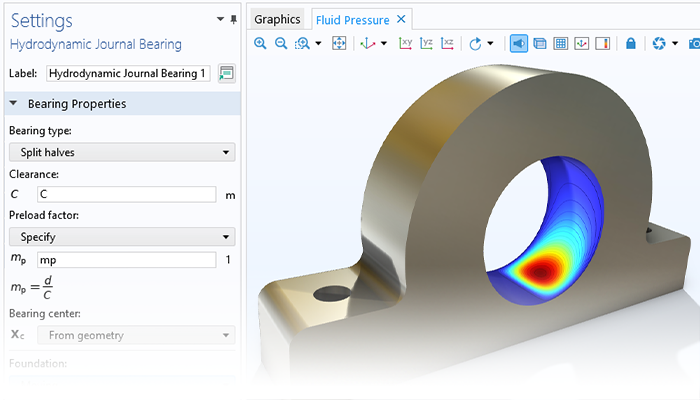
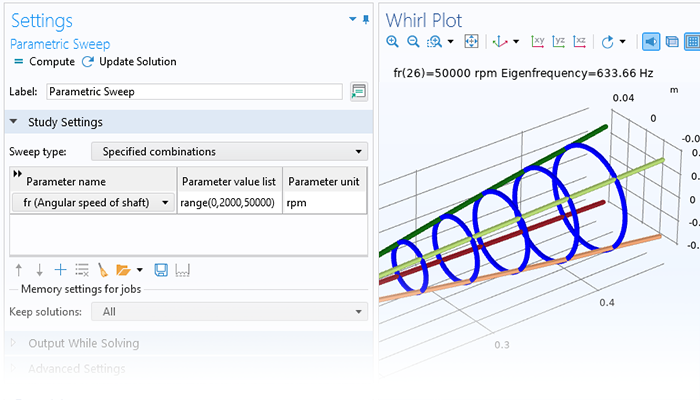
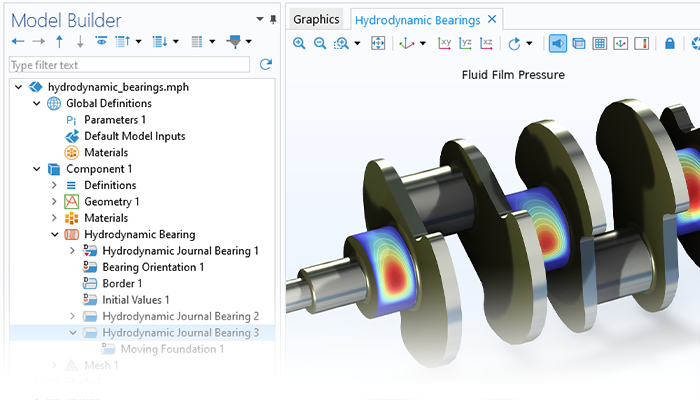
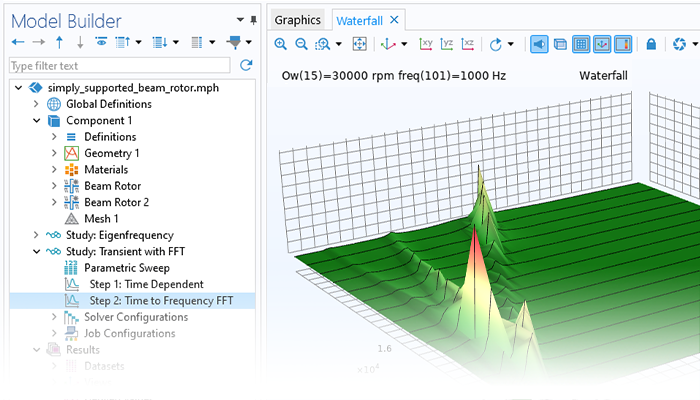
Il Rotordynamics Module consente di analizzare le risonanze, le sollecitazioni e le deformazioni di rotori, cuscinetti, dischi e fondazioni, permettendo agli utenti di mantenere le condizioni entro limiti operativi accettabili. Il modulo può anche essere utilizzato per valutare come i diversi parametri di progettazione influenzino le frequenze naturali e, di conseguenza, le velocità critiche, i vortici e le soglie di stabilità. Inoltre, può essere utilizzato per studiare le risposte di squilibrio stazionarie e transitorie.
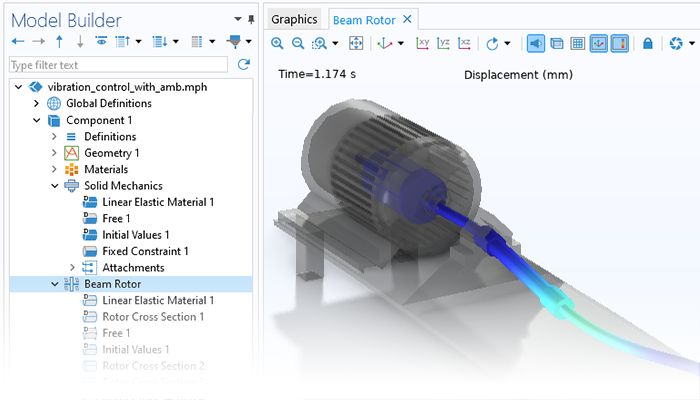
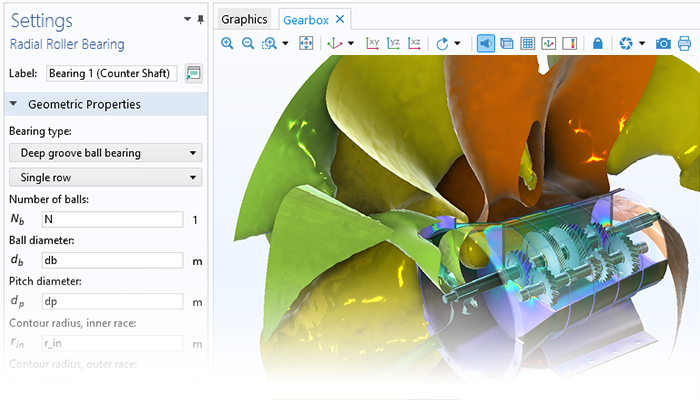
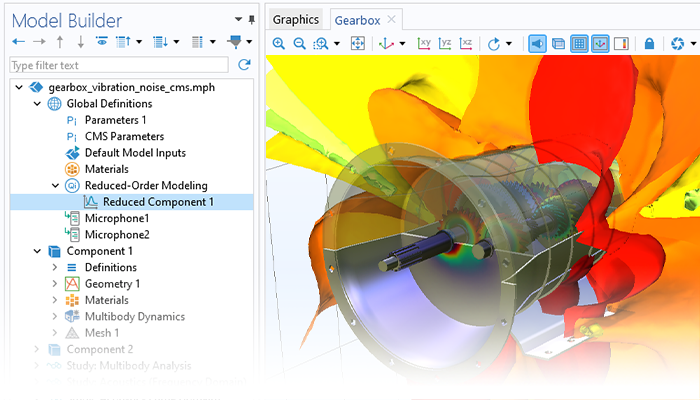
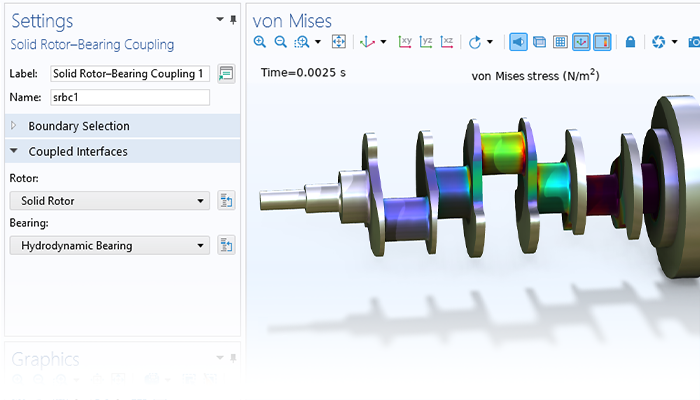
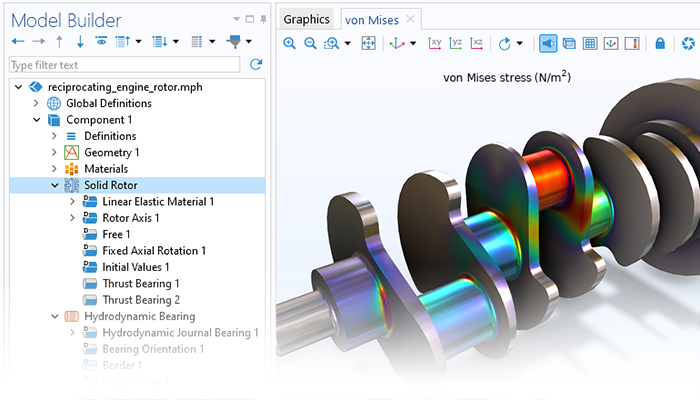
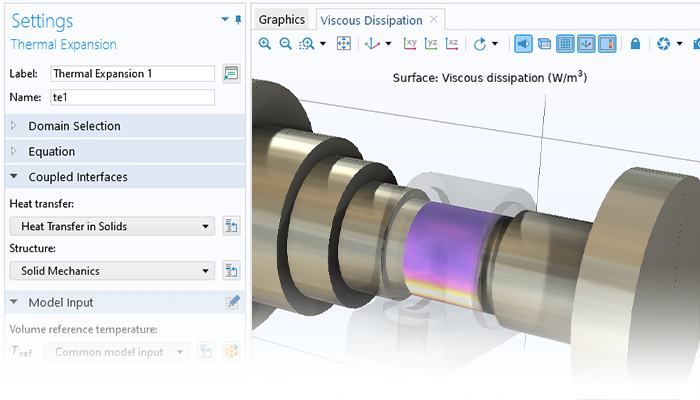
Il modulo fornisce anche funzionalità che possono essere utilizzate per prevedere come il comportamento rotazionale possa portare a sollecitazioni nel rotore stesso e alla trasmissione di carichi e vibrazioni ad altre parti del gruppo della macchina rotante.