
Fractals are those exotic mathematical entities whose geometric properties fall between integer dimensions (1D, 2D, 3D). Space-filling curves and bounded sets with infinite perimeters fall into this category.
Famous Fractals: The Mandelbrot Set and Koch Snowflake
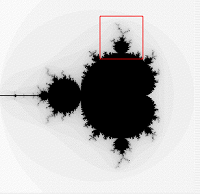
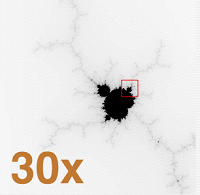
One of the most famous fractals is the Mandelbrot Set, made popular by mathematician Benoit Mandelbrot. This recursively generated set is a great example of the most recognizable characteristic of fractals: self-similarity that persists at arbitrarily small scales. That is, you can look at the Mandelbrot Set and see the shape. Zoom in on the boundary, and, wow, there’s the Mandelbrot Set again! Zoom in again — yep, there it is.
|

|
|

|
The Mandelbrot Set. Image attribution: Agro1986.
The Koch Snowflake (shown below) is another well-known example of a fractal. It’s easy to understand because you can construct it by starting with an equilateral triangle, and then altering each line segment iteratively.
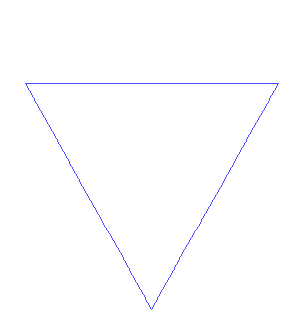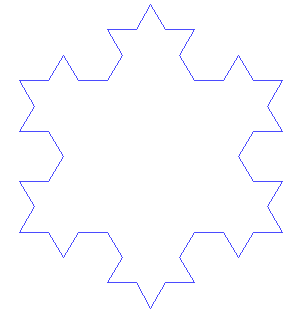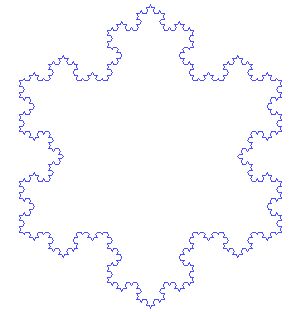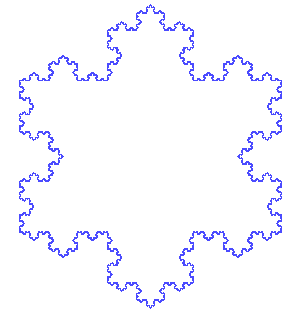
The Koch snowflake.
Engineering Applications
With the onset of computer graphics over the past thirty years, computational methods of generating fractals have made them a popular teaching tool that can open students’ eyes to the beauty of the mathematical sciences. Sure, fractals are beautiful, but it turns out that they’re more than just eye candy.
Fractal structures, in fact, have some desirable properties for engineers doing research in antennas and metamaterials. For RF applications, fractals can generate multiple resonances. Take, for instance, the Sierpinski triangle. This shape is generated by recursively removing the center sub-triangle in an equilateral triangle. The Model Library of the RF Module includes an in-depth analysis of such a fractal monopole antenna.
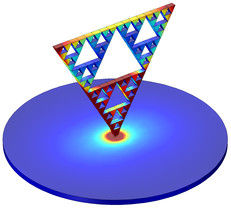
Sierpinski fractal monopole antenna, created using COMSOL Multiphysics and the RF Module.
Fractals also have their place in the emerging field of metamaterials (known in the popular science media for the many cloaking applications). The “magic” behind metamaterials is in the repeating structure that causes “normal” materials to take on “strange” properties (like negative refractive index). It’s pretty clear that the self-similar nature of fractals fits into this category. The precise details of one such example was presented at a recent COMSOL Conference and appears in the proceedings. In their paper, “Designing a Smart Skin with Fractal Geometry“, S. Ni, C.Y. Koh, S. Kooi, and E. Thomas from MIT use a repeating H structure to design a phononic metamaterial with applications to “smart skin” — a type of film with sensors throughout.
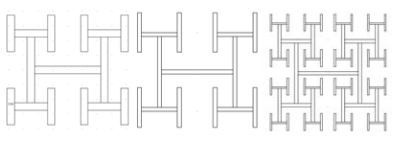
Repeating H pattern in the phononic material. Image courtesy of S.S. Ni, et al.
It might be a while before fractals find their way into everyday products, but these promising results show that beautiful things can be useful, too.





Comments (0)