
If you enjoy ketchup with your food, there’s a good chance you’ve experienced what we’ll call here the all-or-nothing ketchup quandary. You know, that moment when you reach for a new glass bottle of ketchup, remove the cap, and turn the bottle practically upside down — and then nothing happens. Intuitively, you shake or tap the bottle, and then suddenly your food is completely coated in ketchup (unless your reflexes are really good, of course). In this blog post, we explain the all-or-nothing effect of pouring ketchup with a simulation of ketchup flow from a bottle.
Where Is My Ketchup?
Ketchup, in addition to being an exceptionally popular condiment, is also a non-Newtonian fluid. This is the key to its curious behavior. As a non-Newtonian fluid, ketchup’s viscosity — and consequently its ability to flow — varies with the velocity gradient across the fluid or the shear rate. When you first turn the ketchup bottle upside down, it’s probable that you will get only very minimal flow, if any at all, due to its high initial viscosity. Fortunately, ketchup also has an interesting shear thinning property. When an external force is applied in addition to gravity, the increased shear will result in decreasing the ketchup’s viscosity, allowing the product to flow more readily. This is why we sometimes must tap or shake the bottle to enjoy ketchup with our fries.
Simulating a Non-Newtonian Fluid Flow from a Bottle
To satisfy our curiosity, as well as our appetites, and come one step closer to perfecting our ketchup-pouring technique, we have simulated ketchup flow from a bottle using the COMSOL Multiphysics® software and add-on CFD Module. In this simulation, we have made a few simplifying assumptions, including the infinite extent of the bottle (our ketchup lasts forever!), and single-phase laminar flow, thereby ignoring air trapped in the bottle. All velocities presented are in meters per second (m/s).
We specified the geometry of our bottle and boundaries for laminar flow including a no-slip wall, pressure inlet (representing the weight of the portion of ketchup not modeled), and pressure outlet (the external atmosphere) as demonstrated in the figure below.
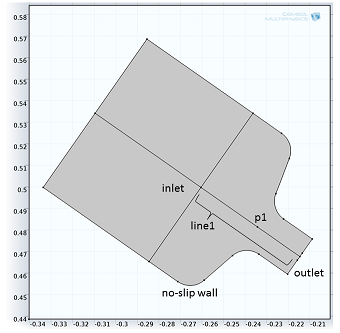
2D geometry used for the simulation. Applied boundary conditions are shown.
We also added the volume force feature to include gravity and the force resulting from shaking the bottle along the y-axis for 0.2 seconds.
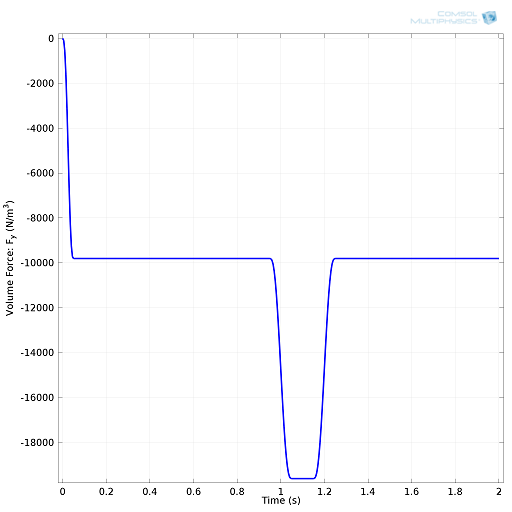
In order to provide the solver with consistent initial conditions, the volume force due to gravity is ramped up from 0 to its full magnitude with a step function (the transition zone is 0.05 seconds wide). The shaking action is simulated with a 0.2-seconds-wide rectangle function. During this interval, the volume forces are doubled.
Pouring Ketchup
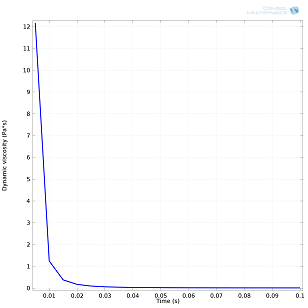
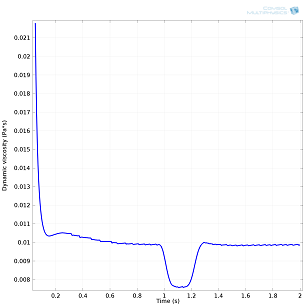
We ran the simulation for a preparation of ketchup based on data available by Koocheki et al. To simulate ketchup flow, we used the non-Newtonian power law to express the dynamic viscosity. The ketchup formulation was simulated by specifying the consistency coefficient and the flow behavior index in the power law equation. The following set of images demonstrates the higher initial viscosity and non-Newtonian flow in a ketchup formulation with 1% added Xanthan gum.
Left: Viscosity measured in p1 (see model setup above) as a function of time, time interval [0,0.1] seconds. Right: Viscosity measured in p1 (see model setup above) as a function of time, time interval [0.1,2] seconds. Shear thinning properties of ketchup are evident, especially during the [1,1.2] second interval when the bottle is shaken. Viscosity decreases, thus allowing more product to flow out of the bottle.
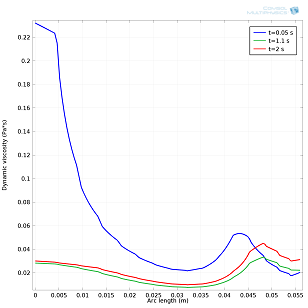
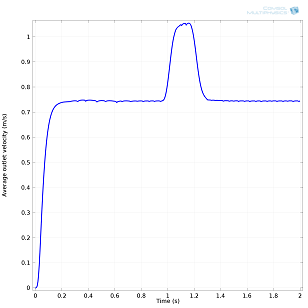
Left: Viscosity measured along line 1 (see model setup above) at three different times. Right: Average outlet velocity as a function of time. It can be seen that the ketchup slowly starts to flow under the action of gravity and then readily increases when the bottle is shaken.
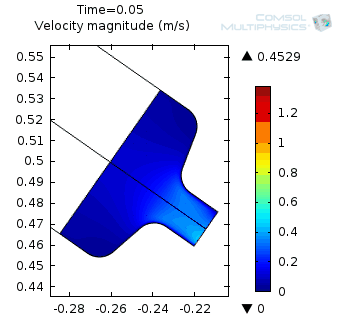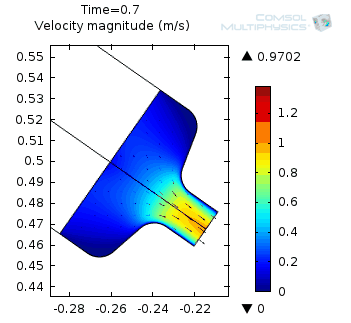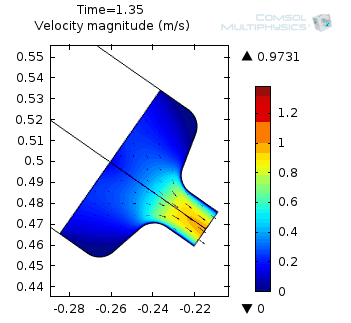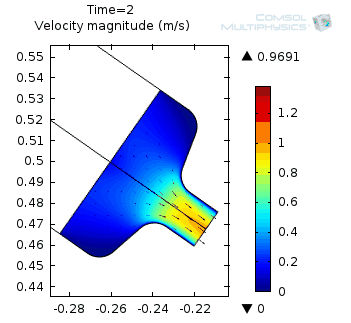
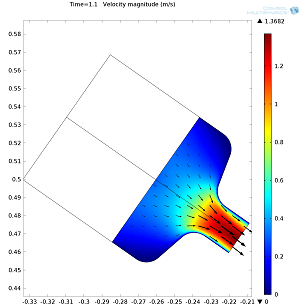
Left: Velocity magnitude animation from 0.05 to 2 seconds. Right: Velocity magnitude at 1.1 seconds.
The All-or-Nothing Ketchup Quandary
Waiting for a change in the flow rate may seem familiar to you. Once the flow rate does start to change, it changes very quickly, resulting in a ketchup deluge that coats our food. The intrinsic increase in flow velocity results in an increasing shear that in turn lowers the viscosity leading to an even higher flow velocity. This is why ketchup seems to be initially stationary but then suddenly flows like water.
The particular subject of ketchup flow from a bottle is more complex than it may seem at first. There are many variables that impact how quickly we experience an all-or-nothing ketchup surprise. If you’re interested in investigating this effect further, I encourage you to experiment with COMSOL Multiphysics and the CFD Module. You could, for instance, study how variables such as tilt angle, air trapped in the bottle, and even bottle design affect the ketchup-pouring experience.



Comments (3)
walid eddaji
November 30, 2021could you please give us more details about this beautiful simulation?
Yusuf Nasir
March 31, 2023Can you share mph/pdf files?
Yogesh Harshe
November 5, 2025can you please share the model ?