The sensing and interpretation of acoustic waves can reveal valuable, hidden information in a variety of objects. The devices that enable us to see wave behavior, such as piezoelectric (PZT) sensors, must be carefully designed and calibrated — a process sometimes called characterization. A Swiss-based research team has used multiphysics modeling to characterize PZT sensors used in acoustical nondestructive testing (NDT) of materials and products. Their project demonstrates how simulation can help make this process more efficient. By optimizing the meshing of the geometry, the team cut their model’s memory demands in half, and reduced computation time by a factor of 5!
Acoustic NDT Reveals Hidden Flaws with Sound
NDT describes a process that reveals important attributes of an object without damaging it. This process is an integral part of development and quality control for many products and systems. NDT methods typically apply a pulse of energy to “interrogate” a structure or material. The energy signal will be changed by cracks or other physical irregularities inside the structure. These changes can be picked up by instrumentation mounted on or near the structure. For example, active thermography involves the application of heat to an object. Internal irregularities can cause unexpected changes to heat distribution, and these changes can be measured and used to locate them.
Acoustic emissions (AE) analysis is another important NDT technique. When applied to a solid object, a wave in the ultrasonic frequency range will be affected by internal cracks and other discontinuities. The resulting changes to the acoustical signal can be picked up by PZT sensors, which produce electric current in response to mechanical pressure. Interpreting the resulting signals, and deriving useful information from them, is an ongoing challenge.
Multiphysics simulation is a natural complement to the AE testing process. By incorporating experimental data into a model of a given material, along with models of wave propagation and PZT sensor responses, researchers can establish a simulated baseline for acoustic signal behavior. Fracture-mechanics-based modeling of material defects, and the impact of these defects on simulated wave behavior, can help predict how PZT sensors will respond to actual discontinuities in further testing. With recent advances, the computational demands of this type of simulation have been dramatically reduced.
PZT Sensors Record the Results of Ball Impact Tests
Whether it’s used to map underground fault lines or a microscopic flaw inside a metal plate, acoustic emissions NDT requires precise characterization of sensing instruments. Researchers at the Swiss Seismological Service, affiliated with the Rock Physics and Mechanics Laboratory at ETH Zurich, built a model in the COMSOL Multiphysics® software to characterize PZT sensors for use in ball impact tests of sheet materials. The apparatus used for these tests is shown below.
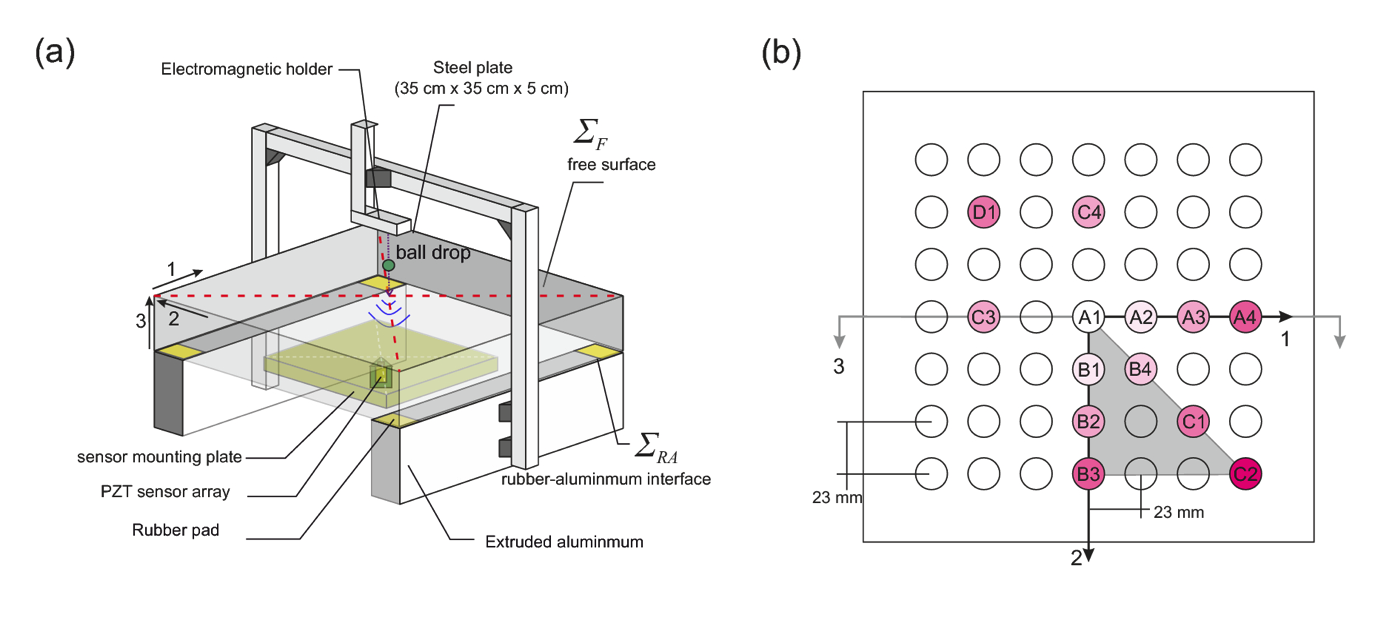
An illustration of the Swiss team’s apparatus for experimental testing of PZT sensors (left). An arrangement of the sensor array in relation to the workpiece (right). Image by R. Wu, P. A. Selvadurai, C. Chen, and O. Moradian. Licensed under CC BY 4.0, via Springer.
When used as part of the characterization process, the testing apparatus drops metal balls of various sizes onto a homogeneous metal workpiece. The impact of each ball generates acoustic waves in the ultrasonic frequency range. By measuring sensor behavior under these controlled conditions, the researchers obtain data for use in the numerical characterization process.

An example of a ball drop test performed in Wu et al (2021).
DG-FEM Modeling Enables Numerical Characterization of PZT Sensors
To obtain useful information from the wave behavior tracked by PZT sensors, researchers can compare test results to the calculated propagation of waves within a semi-infinite homogenous and isotropic elastic plate. The process of calculating how elastic stress waves propagate, based on generalized ray theory, is called “Lamb’s problem”. The solution of Lamb’s problem for a given material, known as “Green’s function”, is a value for the elastic disturbance caused by stress waves due to a point force.
These calculations can help establish a baseline for characterization of PZT sensors, but this approach has significant limitations. In their report published in the Journal of Nondestructive Evaluation, the Swiss research team explains (Ref. 1):
Two main concerns limit the application of the generalized ray theory to calculate Green’s functions. First, the corner frequency of amplitude spectra of in situ AE events could be as low as hundreds of Hz to several kHz. […] This requires large computational loads to obtain the huge number of possible ray paths of Green’s functions. Second, sample finiteness makes the semi-infinite conditions associated with Lamb’s problem unrealistic for laboratory investigations and, therefore, the ray paths of side reflections from a finite elastic plate are nonnegligible.
The team addressed these concerns through the time explicit, discontinuous Galerkin finite element method (dG-FEM) modeling in COMSOL Multiphysics. A simulation-based approach enabled them to obtain values for Green’s functions within boundary conditions comparable to those of a finite, real-world test case.
Optimizing Mesh to Lower the Computational Cost of Simulation
The PZT characterization model was built using the Elastic Waves, Time Explicit interface, which can be used to model the propagation of elastic waves over large intervals containing many wavelengths. The model numerically calculates true Green’s functions from 1 kHz to 1 MHz, excited by a Heaviside step force-time function. It uses a relatively fine mesh to find Green’s functions for high-frequency waves, and a coarser mesh to find Green’s functions of low frequency. The mesh optimization process, and its positive impact on computational efficiency, is explained further below.
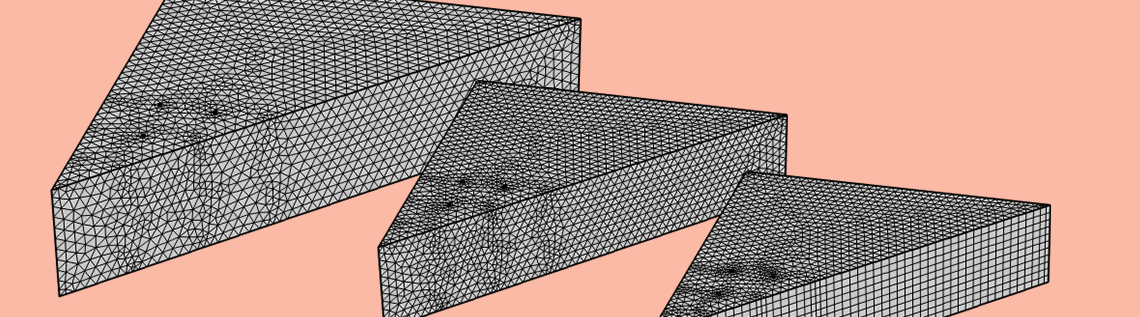
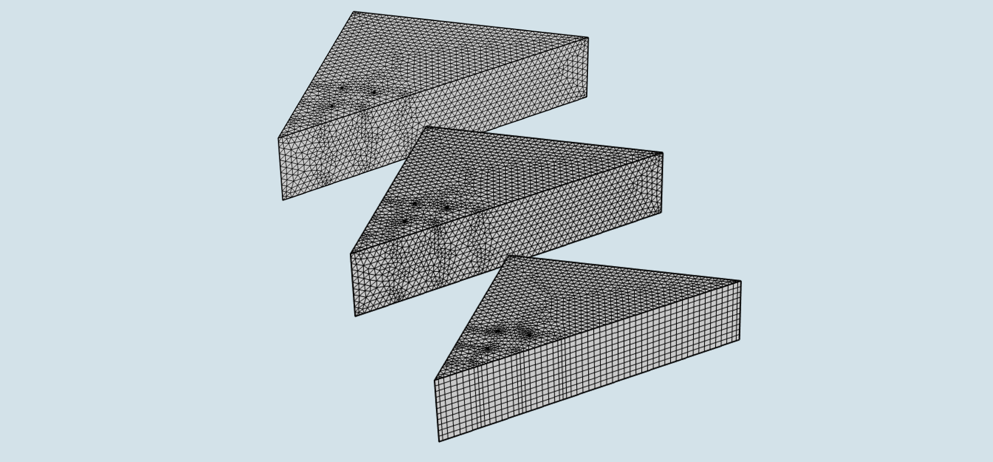
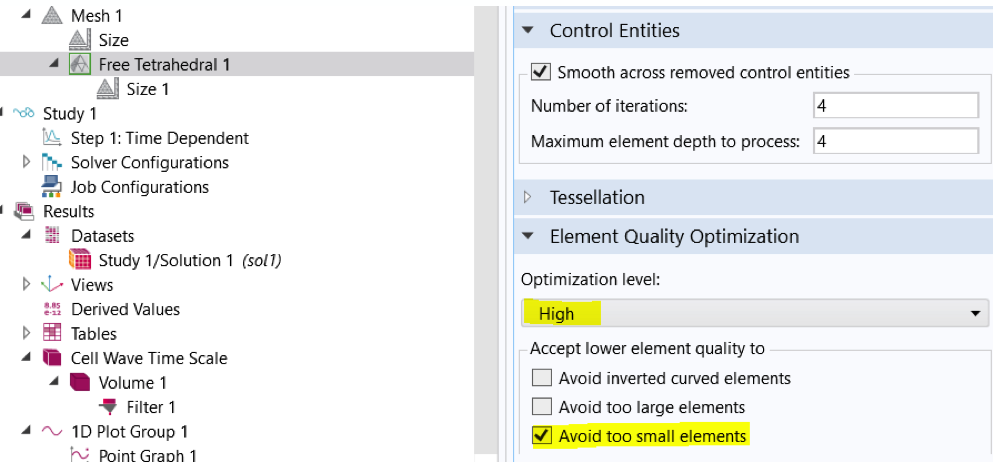
An illustration of three meshes applied to a section of workpiece for a simulated ball drop test. Denser mesh zones on all three indicate the points at which PZT sensors will be mounted. At right, a screenshot of the Elastic Waves, Time Explicit interface showing the Avoid too small elements mesh optimization tool.
When modeling using the time explicit dG-FEM formulation, the time step taken by the solver is governed by the smallest value of the mesh element size metric relative to the maximum wave speed (typically the pressure wave speed in solids). This means that careful meshing is important to get optimal performance. In the image above to the left, the three meshes, from top to bottom, show progressive steps in the optimization process. The mesh at the top shows a free tetrahedral mesh with a refinement at the locations of PZT sensors for the lab test. The center mesh shows slight changes as a result of using the Avoid too small elements tool (computation time reduced by a factor 2). In the mesh at the bottom, we see further simplification, as the triangular mesh is swept across an 11-layer horizontal plane. The structured mesh resulted in a reduction in degrees of freedom (DOFs) and helped cut the model’s memory demand by a factor of 2, and its computational time by a factor of 5.
Of course, a simplified mesh wouldn’t be helpful if it compromised model performance. Fortunately, the three models all showed nearly identical results in response to a simulated wave at two measurement points. Further optimization is achieved through the use of coarser mesh for measuring simulated waves of longer wavelengths, as shown below.
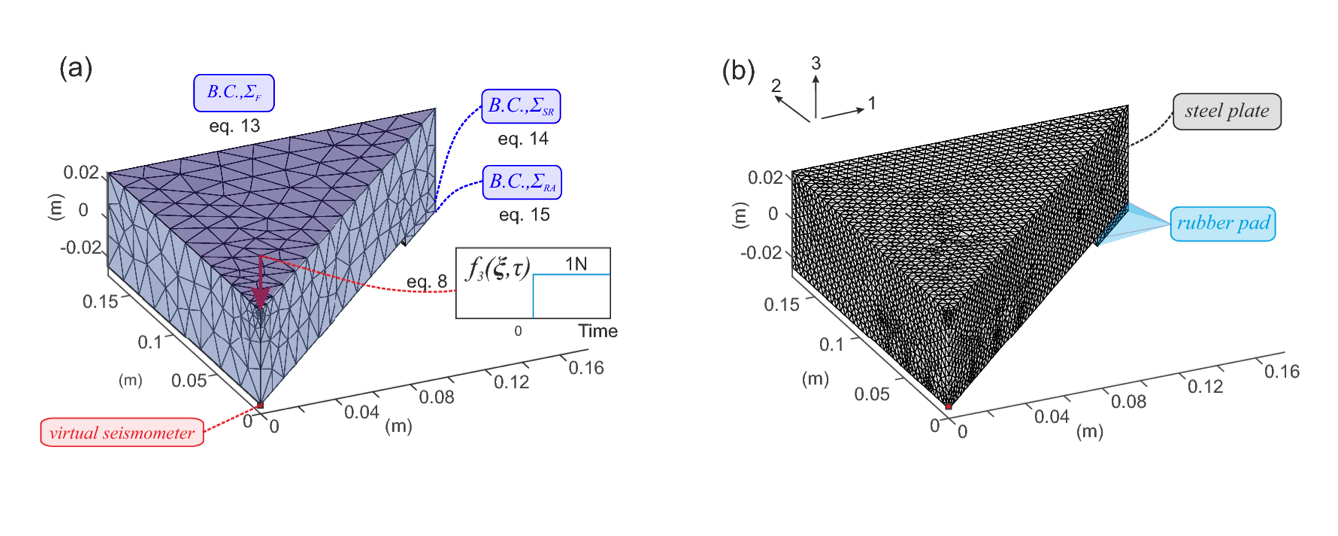
On the left, a coarse mesh for simulation of low-frequency wave propagation across a modeled steel plate. High-frequency simulated wave behavior is captured using the finer mesh shown on the right. Image by R. Wu, P. A. Selvadurai, C. Chen, and O. Moradian. Licensed under CC BY 4.0, via Springer.
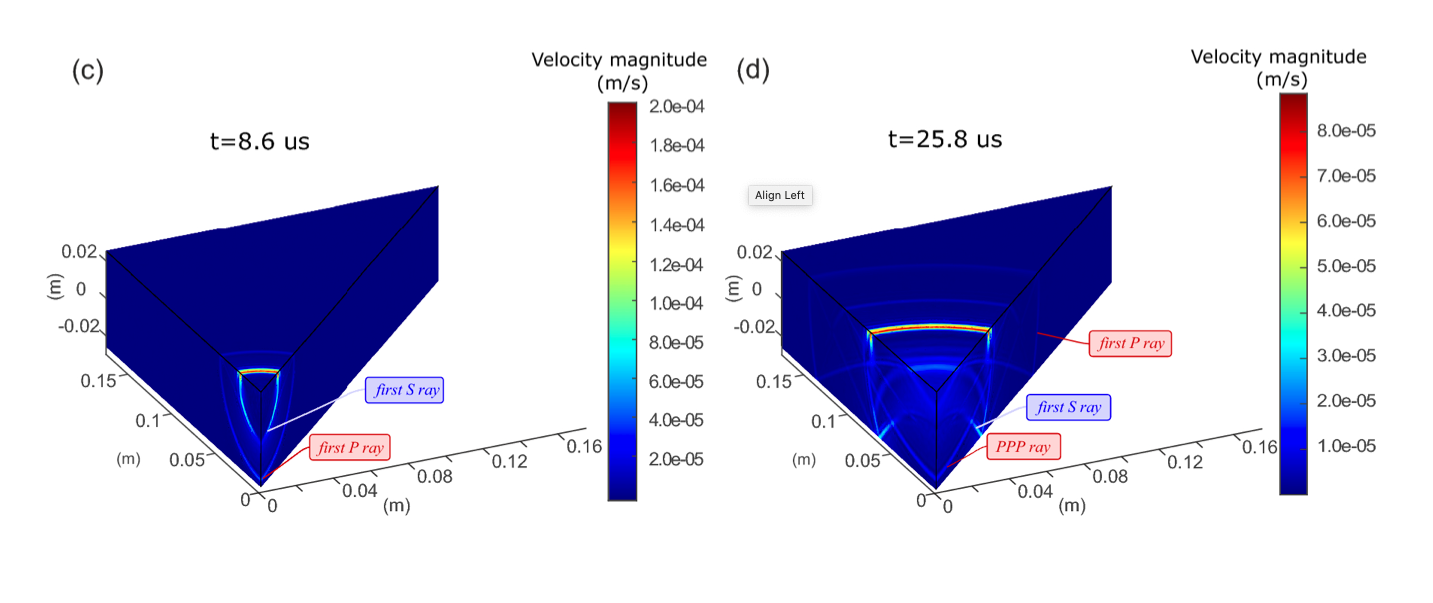
Magnitude of a particle motion velocity field, as simulated using the fine-mesh model, at 8.6 nanoseconds (left) and 25.8 nanoseconds (right). Image by R. Wu, P. A. Selvadurai, C. Chen, and O. Moradian. Licensed under CC BY 4.0, via Springer.
Next Steps for Further Study
After experimental testing based on their modeling, the team affirmed that their dG-FEM-based process enables them to “absolutely calibrate PZT sensors and thus properly interpret the messages of ground motion from AE monitoring.” (Ref. 1) Looking ahead, they plan to refine their models to enable further study of fracture propagation in a range of materials.
Related Resources
- Try this tutorial model:
- Check out these blog posts and video:
Reference
- R. Wu, P. A. Selvadurai, C. Chen, and O. Moradian, “Revisiting Piezoelectric Sensor Calibration Methods Using Elastodynamic Body Waves,” Journal of Nondestructive Evaluation, vol. 40, no. 68, 2021, https://doi.org/10.1007/s10921-021-00799-1



Comments (0)