
Engineers working with lasers, optical fibers and waveguides, nonlinear optical processes, metamaterials, and other large photonic devices ultimately deal with wave optics. Photonic devices are considered “large” when they are larger than a wavelength of light. In that case, you deal with optics frequencies as opposed to radio frequencies, and the device is not complex enough to justify approximating with rays.
Wave Optics, Working with Wavelengths
We should all be familiar with this equation: speed of light = wavelength * frequency. Engineers and researchers working within wave optics concern themselves with the wavelength aspect of the equation; they treat light as a wave. Many optical devices are much larger than the wavelength of light that is passed through the component — compare the wavelength of a micrometer to the millimeter- to centimeter-sized optical device.
If you are working with structures that are a lot larger than the wavelength — even larger than the ones I just mentioned — you can, of course, approximate light with rays (this application area is referred to as ray optics). In that case you assume the wavelength to be 0, and the frequency infinite. You can do that because it is easy to follow the rays to see where they go, and you do not consider diffractive effects as you do in wave optics.
Modeling Large Photonic Devices using a Paraxial Optical Propagation Method
In 2009 we received a paper submission for the COMSOL Conference in Boston, titled “Implementation of a Paraxial Optical Propagation Method for Large Photonic Devices“. As the author of this paper spells out, simulating large photonic devices was at the time not that simple.
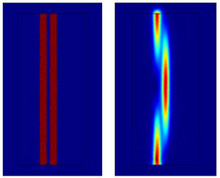
Symmetrical directional coupler:
Refractive index distribution (left)
and optical intensity (right).
Image originally produced by
J.E. Toney, Pennsylvania State University
Electro-Optics Center, Freeport,
Pennsylvania, USA.
“The greatest computational limitation of the finite element method for modeling electromagnetic waves is the need for a mesh that is finer than the wavelength, λ,” he writes. This is true: if you’re using the RF Module, the element size needs to be smaller than the wavelength, and if the geometry is large, and the number of wavelengths encompassed by it many, then a lot of mesh elements would be required to resolve the modeling domain. The author of this particular paper figured out a work-around to this problem, by utilizing a paraxial optical propagation method for modeling photonic devices. Using this method, the researcher was able to simulate large photonic devices, as it allowed a coarser mesh than other electromagnetic propagation modes. One thing that strikes me about this research, though, is that the method is similar to the Beam Propagation Method (BPM).
Approximations Can Lead to Inaccuracies
If you are presently working with laser design, nonlinear optics, fiber optics, and the like, you’re likely already familiar with the BPM. This method uses the slowly varying envelope (SVE) approximation, which unfortunately leads to inaccuracies when trying to simulate the propagation of light in real devices having a high refractive-index contrast. When attempting to accurately model discretely varying structures, again this method comes up short.
So what can a wave optics engineer do? I suppose it would be nice to apply the theory of BPM but to avoid the approximations therein. Today’s computers, having tens or hundreds of GB of RAM, should be able to handle this better now compared to 15 years ago when BPM started to show up in commercial software.
Soon we’ll be able to share some exciting news on this topic with you, so be sure to check back with us on the blog shortly.




Comments (0)