Blog Posts Tagged Technical Content
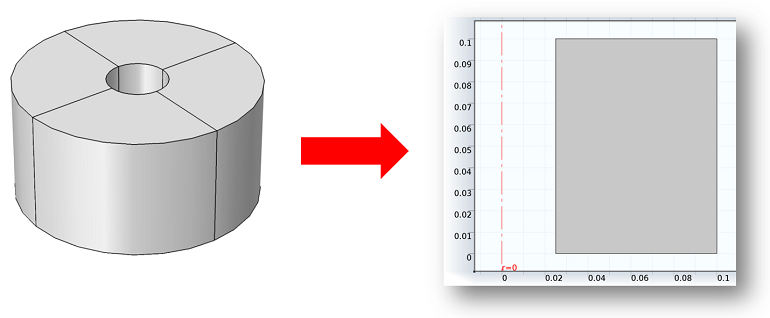
Parameterizing the Dimensions of Imported CAD Files
Learn how to modify an imported geometry with some clever usage of the Deformed Geometry interface in COMSOL Multiphysics®.
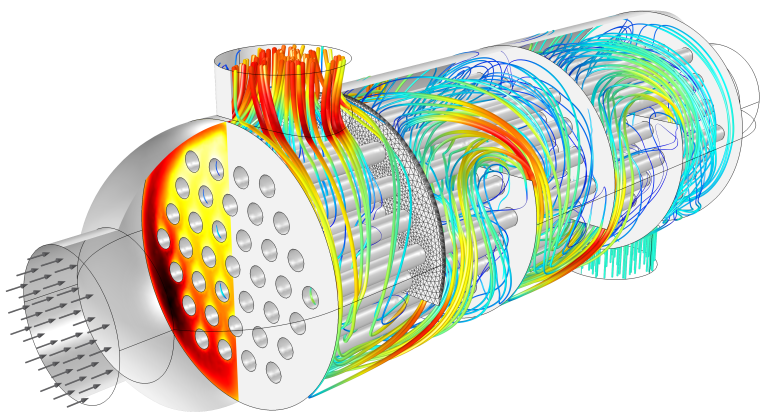
Conjugate Heat Transfer
Get an introduction to the concept of conjugate heat transfer and see some of its applications and modeling considerations.
MEMS Microphone Model Presented at ASA 166 in San Francisco
What is a MEMS microphone? Learn about this versatile device, as well as how to model it using COMSOL Multiphysics® with the add-on MEMS Module and Acoustics Module.

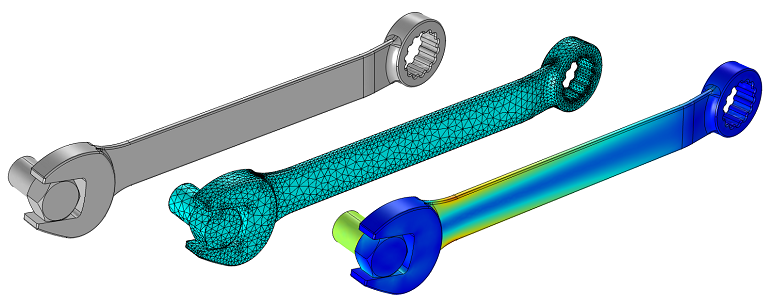
Submodeling: How to Analyze Local Effects in Large Models
Modeling a particularly large structure with a lot of boundary conditions? Learn how to use submodeling, a technique for analyzing local effects in large models in COMSOL Multiphysics®.
Visualization for 2D Axisymmetric Electromagnetics Models
Today we’ll look at how to make 3D plots of vector fields that are computed using the 2D axisymmetric formulation found in the Electromagnetic Waves, Frequency Domain interface within the RF and Wave Optics modules.

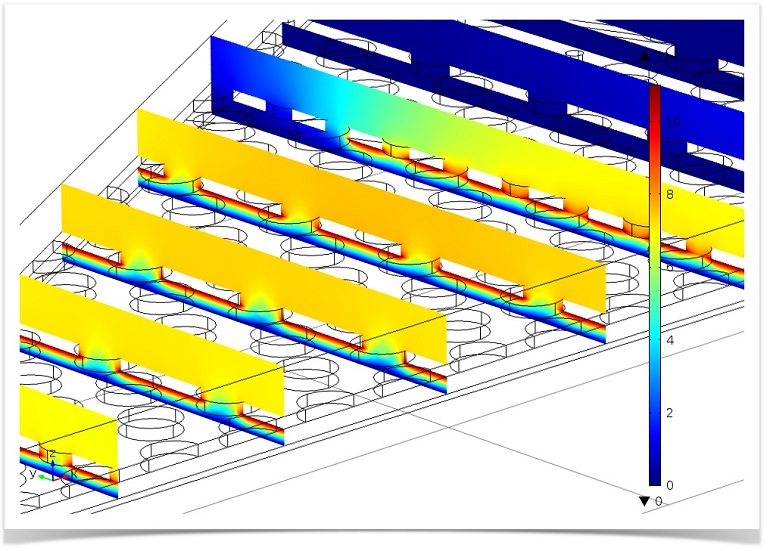
Using Adaptive Meshing for Local Solution Improvement
One of the perennial questions in finite element modeling is how to choose a mesh. We want a fine enough mesh to give accurate answers, but not too fine, as that would lead to an impractical solution time. As we’ve discussed previously, adaptive mesh refinement lets the software improve the mesh, and by default it will minimize the overall error in the model. However, we often are only interested in accurate results over some subset of the entire model space. […]
Learning to Solve Multiphysics Problems Effectively
One of the questions we get asked often is how to learn to solve multiphysics problems effectively. Over the last several weeks, I’ve been writing a series of blog posts addressing the core functionality of the COMSOL Multiphysics software. These posts are designed to give you an understanding of the key concepts behind developing accurate multiphysics models efficiently. Today, I’ll review the series as a whole.
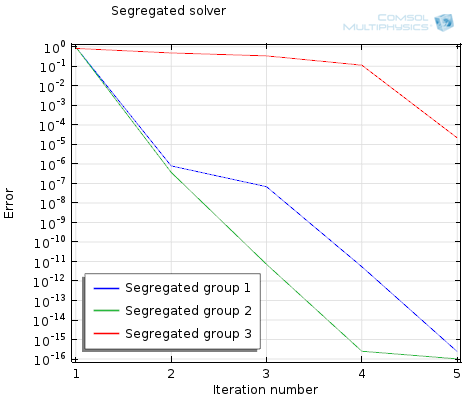
Improving Convergence of Multiphysics Problems
In our previous blog entry, we introduced the Fully Coupled and the Segregated algorithms used for solving steady-state multiphysics problems in COMSOL. Here, we will examine techniques for accelerating the convergence of these two methods.
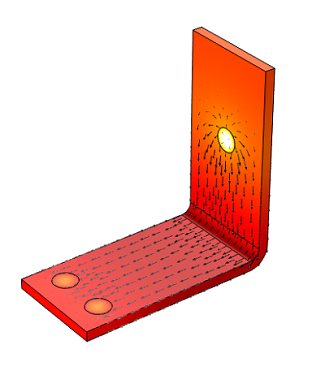
Solving Multiphysics Problems
Here we introduce the two classes of algorithms used to solve multiphysics finite element problems in COMSOL Multiphysics. So far, we’ve learned how to mesh and solve linear and nonlinear single-physics finite element problems, but have not yet considered what happens when there are multiple different interdependent physics being solved within the same domain.

Thermal Modeling of Surfaces with Wavelength-Dependent Emissivity
Whenever we are solving a thermal problem where radiation is significant, we need to know the emissivities of all of our surfaces. Emissivity is a measure of the ability of a surface to emit energy by radiation, and it can depend strongly upon the wavelength of the radiation. This is very relevant for thermal problems where the temperature variation is large or when there is exposure to a high-temperature source of radiation such as the sun. In this post on […]
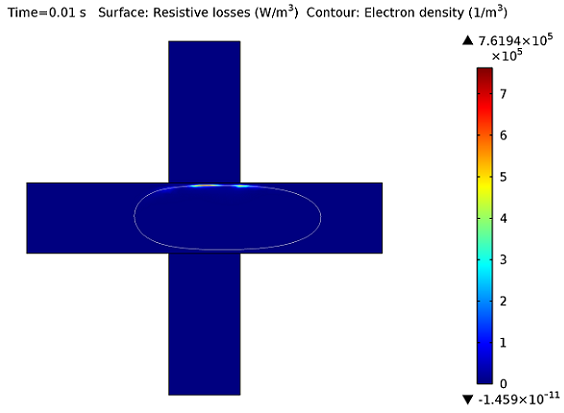
Microwave Plasmas
Microwave plasmas, or wave-heated discharges, find applications in many industrial areas such as semiconductor processing, surface treatment, and the abatement of hazardous gases. This blog post describes the theoretical basis of the Microwave Plasma interface available in the Plasma Module.
Meshing Considerations for Nonlinear Static Finite Element Problems
As part of our solver blog series we have discussed solving nonlinear static finite element problems, load ramping for improving convergence of nonlinear problems, and nonlinearity ramping for improving convergence of nonlinear problems. We have also introduced meshing considerations for linear static problems, as well as how to identify singularities and what to do about them when meshing. Building on these topics, we will now address how to prepare your mesh for efficiently solving nonlinear finite element problems.
