Latest Posts

Efficiently Distribute Lightweight Compiled Applications
Have you ever tried to send an email but the attachment was too large? COMSOL Compiler™ has an option that reduces the file size of standalone applications for more efficient distribution.
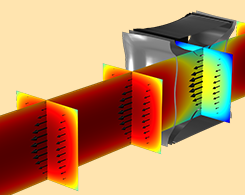
Three Semiconductor Device Models Using the Density-Gradient Theory
You can use the density-gradient theory to model semiconductor devices. Here are 3 examples: a Si inversion layer, Si nanowire MOSFET, and InSb p-channel FET.

Photos from the COMSOL Conference 2019 Beijing
This past fall, nearly 500 members of the COMSOL community attended the COMSOL Conference 2019 Beijing to partake in keynote speeches, user presentations, minicourses, and more.

Intro to Density-Gradient Theory for Semiconductor Device Simulation
The density-gradient theory is a computationally efficient way to include quantum confinement in the conventional drift-diffusion formulation commonly used for simulating semiconductor devices.
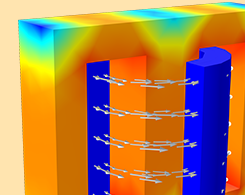
How the B-H Curve Affects a Magnetic Analysis (and How to Improve It)
Magnetic soft iron steels are widely used as core materials in motors, transformers, and inductors. The B-H curve is used to describe the magnetization properties of such materials.

Evaluating Stress and Thermal Expansion in a Portal Crane
As extreme heat waves increase in frequency, it is important to consider thermal expansion when designing bridges. With COMSOL Multiphysics®, you can.

Happy Birthday, Andrew Fielding Huxley
As a child, Andrew Fielding Huxley was given a lathe as a gift. This sparked an interest in science and invention that blossomed into a career in research and physiology.
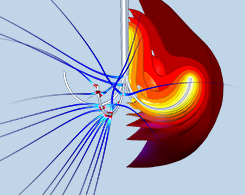
Heat Transfer in Biological Tissue with Thermal Damage Analysis
Hepatic tumor ablation using radiofrequency heating, microwave coagulation therapy, and other cancer treatments can be studied by modeling the electromagnetic heating of biological tissues.
