
A sphere slightly lighter than water is dropped into a small liquid-filled beaker. How do you model the resulting shape of the water surface and the motion of the sphere as it floats on the surface? In this blog post, we demonstrate how to model this system in the COMSOL Multiphysics® software. Although we are considering the case of a small sphere, the technique discussed here can be applied to other larger shapes as well.
Oscillating Motion of a Buoyant Sphere: A CFD Problem
Let’s consider a buoyant sphere that is dropped into a water-filled beaker. The sphere, with a radius of 0.15 cm and density of 800 kg/m3, is initially suspended in air. The cylindrical beaker has a radius of 0.65 cm, a height of 1.7 cm, and is partially filled with water. The size of the system is small enough to assume laminar flow and also allows for a faster solution process on a regular PC. A larger system can be modeled in exactly the same way, but would require more computational resources.
To model the motion of the sphere through the water surface, we need to model the fluid flow in both the air and water phases. If we consider the sphere to be rigid, we can compute the motion of it by solving the ordinary differential equations (ODEs) of motion that account for the force experienced by the sphere falling through the air, hitting the water surface, and finally interacting with both air and water. The total fluid stress exerted by the fluids on solid boundaries is given by
(1)
where ufluid denotes the fluid velocity field, p the fluid pressure, μ the dynamic viscosity of the fluid, n the outward normal to the boundary, and I the identity matrix.

Buoyant sphere suspended in air above the water surface in a water-filled beaker. Part of the beaker wall has been hidden to show the sphere.
Assuming that the solid only moves in the vertical direction (z), we can write
(2)
F_z &= m g + m\frac{d v_{s}}{d t}\\
v_s &= \frac{d u_s}{d t}
\end{align}
where m denotes the mass, vs the velocity in the z direction, and us the displacement in the z direction of the sphere.
The force Fz can be calculated by integrating the z-component of \mathbf{f} from Eq. 1 over the surface of the sphere. The above equations of motion (ODEs) are solved along with the finite element model to compute the displacement and velocity of the sphere.
Since the sphere moves through both air and water, a two-phase flow model is formulated on a spatial frame with time-dependent spatial coordinates to model both fluids. The spatial frame is the usual fixed global Euclidean system with spatial coordinates (x, y). These spatial coordinates, corresponding to the mesh nodes of the fluid domains, are functions of time and represent the current location of a point in space. This is achieved by solving the fluid flow problem on a Moving Mesh interface.
The mesh, on which the fluid flow problem is solved, deforms with a mesh deformation that is equal to the displacement of the sphere at the interfacing boundaries between the sphere and the fluid domains. Inside the fluid domains, the mesh deformation is computed using an appropriate smoothing method that is available in the Moving Mesh interface.
(3)
On the fluid boundaries interfacing the sphere, the fluid velocity is given by
(4)
Setting Up the Model in COMSOL Multiphysics®
We can set up the above problem as a 2D axisymmetric analysis. To model this problem, we couple a Two-Phase Flow interface with a Moving Mesh interface and Global Equations by defining the coupling expressions illustrated in Eqs. 1–4.
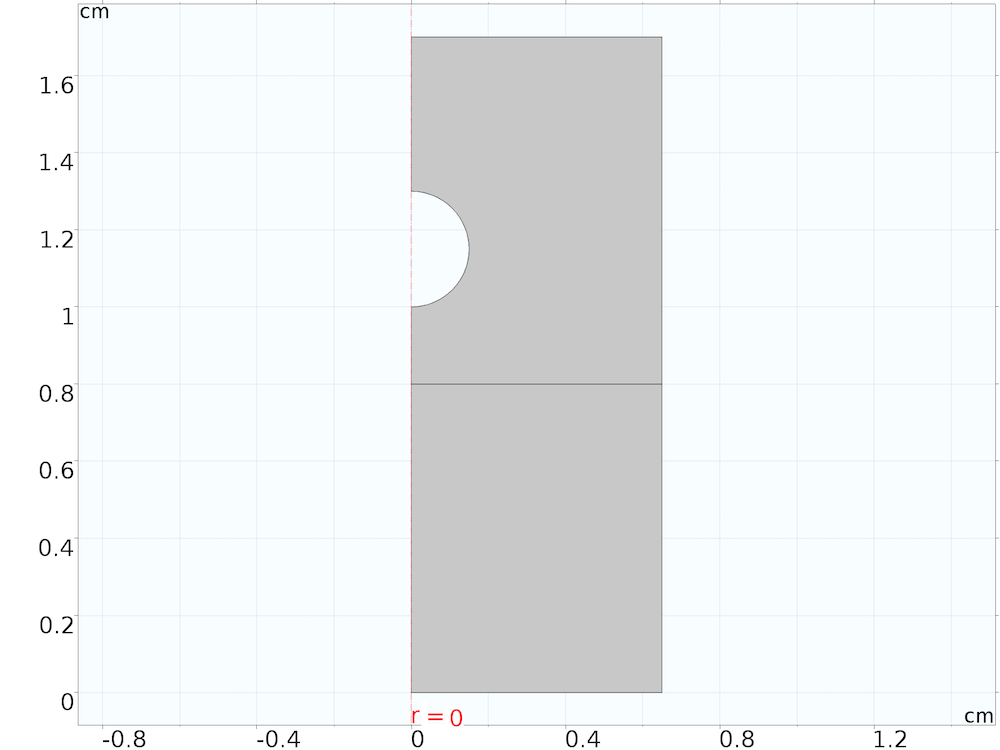
Geometry of the 2D axisymmetric model showing the initial position of the water surface represented by the horizontal line. The sphere is represented as a boundary in the model domain because we are modeling it as a rigid object using ODEs.
The fluid flow in this case is laminar, in both the air and water phases, so we can use the Laminar Two-Phase Flow, Phase Field interface. (Read this blog post on how to choose a multiphase flow interface for more information.) This multiphysics interface automatically defines a coupling between the laminar flow and phase field method, which is used to track the detailed shape of the water surface.
The Laminar Two-Phase Flow, Phase Field interface enables us to model the boundaries of the sphere as moving wetted walls. The Wetted Wall boundary condition of the Phase Field interface lets us specify the contact angle between the water surface and the solid walls, while the Wall Movement setting in the Wall boundary condition of the Laminar Flow interface lets us specify the velocity of the moving solid walls. An Outlet boundary condition is used for the boundary corresponding to the top of the beaker.
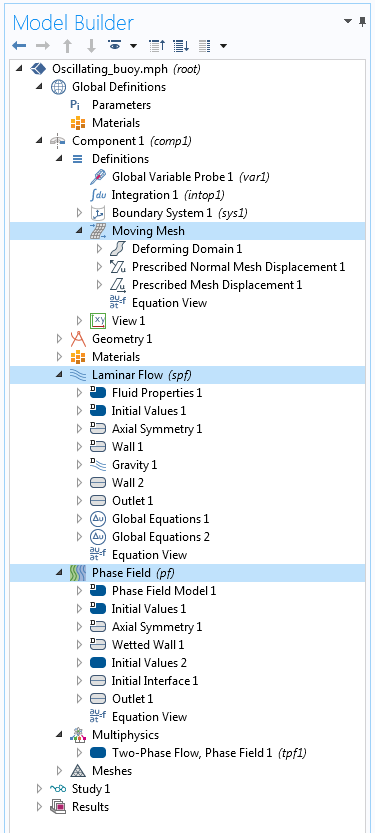
The structure of the model setup and the various interfaces — namely Laminar Flow, Phase Field, and Moving Mesh — is shown in the screenshot below:
In the Phase Field interface, we specify the value of the phase field variable as Φ = 1 (air for Fluid 1) and Φ = -1 (water for Fluid 2) for the initial configuration, along with the boundary representing the initial position of the water surface with the air above and the water below the horizontal line. The initial configuration is shown in the figure above.
We use a Wetted Wall boundary condition to specify the contact angle between the air-water interface, solid walls of the beaker, and sphere. For simplicity, we assume the same contact angle for both the sphere and walls of the beaker.
The velocity field in the fluids is automatically coupled to the phase field method to account for advection. The properties of the fluids and surface tension coefficient are specified in the multiphysics coupling between the Laminar Flow and Phase Field interfaces.
The Moving Mesh interface solves for the mesh deformation within the fluid domains due to movement of the sphere. We also use boundary conditions to describe how the mesh at the fluid boundaries should deform. The important boundary condition here is Mesh Displacement, which is equal to the sphere’s displacement on the spherical boundaries (Eq. 3).
The movement of the sphere is purely due to the gravitational load. However, the fluid exerts a drag force as defined by Eq. 1. The z-component of this force can be computed by integrating the built-in variable for total fluid stress in the z direction over the sphere boundaries. The built-in variable spf.T_stressz computes the total stress in the z direction that is exerted on the sphere boundary by the surrounding fluid.
Learn more in this blog post on how to compute lift and drag.
The ODEs (Eq. 2) are solved using the Global Equations interface. The screenshot below shows one of the equations implemented in the Global Equations interface, where vs is the velocity of the sphere as noted in Eq. 2, vst is the time derivative of velocity (or the acceleration), and intop1 is an integration operator defined over the solid boundaries.
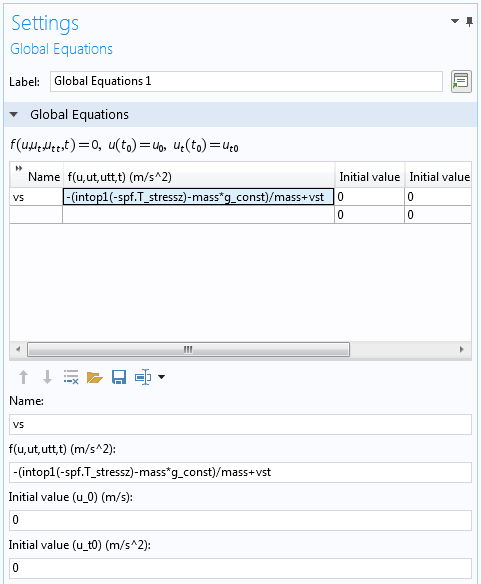
Settings of the Global Equations interface used to solve for the velocity of the sphere.
Since there is a large movement of the sphere, the mesh deformation will be large. To help keep the element quality high and avoid inverted elements, we can use the Automatic Remeshing feature, which stops a transient simulation based on a mesh quality metric and remeshes the current deformed shape before it continues.
Analyzing the Simulation Results
The plot below shows the sphere falling on the water surface, the water-air interface (Φ = 0.5), and a cross-sectional plot of the fluid velocity magnitude.
Animation of the movement of the buoyant sphere in the water-filled beaker, the water surface, and the fluid velocity magnitude plotted on a cross-sectional slice. To see the variation in velocity magnitude at later stages of the simulation, the maximum value of the color scale is capped at 0.1[m/s].
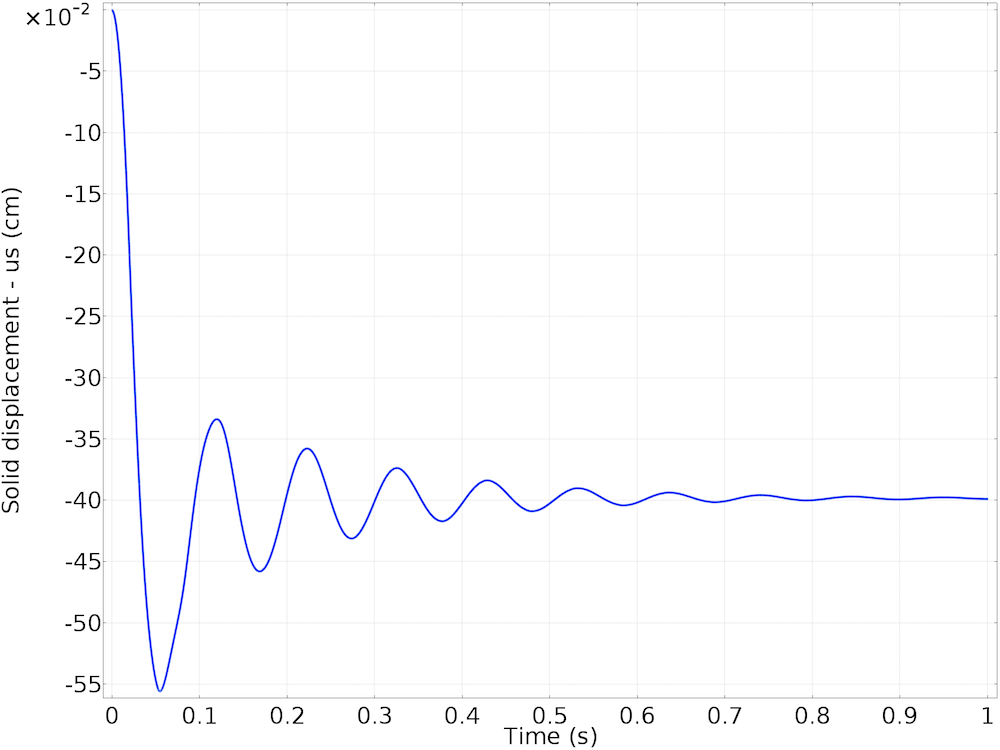
The figure below shows the plot of the displacement of the sphere versus time. As expected, its motion is damped by the fluid surrounding it and the displacement amplitude decreases exponentially with time.
Concluding Thoughts
In this blog post, we have demonstrated how to model the oscillating motion of a buoyant sphere. Here, the sphere and its motion are considered axisymmetric with no rotational motion. In general, should the situation require, the same strategy discussed here can be applied to model both rotation and translation. Modeling such a case would require solving for additional rotational motion of the rigid object using ODEs. It would be much easier to instead use the built-in functionality of the Solid Mechanics interface to automatically solve for the rigid body motions. This would also allow for modeling a larger system where the flow becomes turbulent and the motion can take place in all directions.
Access the file for the model featured in this blog post by clicking the button below:




Comments (13)
Ajay Dusane
January 17, 2018Hi,
Thank you for an exciting blog. I am facing an issue while trying to run the mph file (‘cleared’). I updated my COMSOL Multiphysics software, yet it is unable to run the file. Can you upload it to a previous version?
Thank you!
Ajay Dusane
January 17, 2018I was able to open the file for 5.2 but not for 5.3.
Chandan Kumar
January 18, 2018 COMSOL EmployeeDear Ajay,
The model file associated with this blog is available in version 5.3a. This is not available in version 5.3. Please upgrade your COMSOL installation to the most recent version: https://www.comsol.com/release/5.3a
Best regards,
Chandan
Behnam Nasrollahzadeh
February 3, 2018Hi Mr. Chandan,
Thank you for a blog, I have download the “Oscillating_sphere_cleared.mph” from the comsol site and just run it in COMSOL 5.3a, but i have encountered an error “Internal error callback”. what is the reason of this error? and how i can solve this?
Best regards,
Nasrollahzadeh
Jean-Christophe LOUDET
June 20, 2018Dear Chandan Kumar,
Thank you for this nice blog.
However, I have a question concerning the vertical force balance you wrote in Eq. (2). To me, it seems like there is a term missing: When the particle contacts the fluid interface, in addition to the pressure force you wrote (Fz with Eq. (1)), and which comes from the total stresses generated by fluid motion, a surface tension force acting along the contact line should appear as well, right ?
Thank you very much for your response on this point.
Best regards,
Chris Loudet
Chandan Kumar
June 29, 2018 COMSOL EmployeeDear Jean,
The surface tension forces are already accounted for in the total fluid force. The surface tension force is actually implemented using a volumetric force but multiplied by a dirac delta function which is located at the moving interface. So the fluid stress that is calculated within COMSOL already considers the effect of such a force and any other volumetric force (like gravity for instance) that you would have in the model.
Best regards,
Chandan
Olav Gaute Hellesø
August 29, 2018Dear Chandan,
I would like to comment on the question from Chris Loudet and your reply. It is correct that the surface tension force on the fluid is included in the model. However, the capillary force on the bead is not taken into account. For a demonstration of this, change the units from cm to mm and put the wetting angle on the right-hand wall to 5*pi/6. This causes the bead to bounce off the surface of the liquid and shoot up to hit the ceiling of the model. This is clearly not physical as the bead gains energy. Based on advice from Chris Loudet and a paper (N.O. Jaensson et al, Langmuir 2018, 34, 1795-1806), I added a term for the capillary force in the equation of motion for the bead. This gives a damped oscillation, similar to that for your model in cm. It shows that for a cm-sized bead, the capillary force is not significant, while it is for mm-sized beads.
Best regards,
Olav
Chandan Kumar
August 29, 2018 COMSOL EmployeeDear Olav,
The model uses the two phase flow interface. The two phase flow interface in COMSOL includes the capillary effects as well. See for example: https://www.comsol.com/model/capillary-filling-level-set-method-1878 It is possible that what you are seeing might be related to numerical issues in the model. In any case, for further discussion for the particular size scale you are modeling please contact support@comsol.com
Best regards,
Chandan
AKHIL NATH C K
January 9, 2019Hi, I am new to COMSOL. Could you please guide me how to go about designing a similar setup with a water ball falling on to a metal surface?
Chad Curtis
December 8, 2020The MPH file no longer seems to be available, no? All I see is a Powerpoint. This would be very helpful!
Sanjeev KM
December 18, 2020Hi,
The .mph file is only present for COMSOL 5.6. It would be very helpful if I get it for version 5.5.
Xin Jin
September 21, 2022Excellent tutorial!
Oussamane Mebarako
June 27, 2024is it possible to get the sphere instant velocity plot ?