
The Newman model and its variants form the standard theory used to successfully predict the behavior of lithium-ion battery design under a range of operating conditions. In the Newman model, the geometry of the porous structure of the battery electrodes is not described in detail; instead, typical averaged dimensions are used as input to describe the electrodes as homogeneous and isotropic materials. But how accurate is this approach compared to a detailed, heterogeneous geometric model? Let’s find out.
Different Approaches to Modeling Lithium-Ion Batteries
The field of lithium-ion battery modeling is dominated by the Newman model and its variants. These models are based upon the homogenization of porous structures: You avoid having to draw the detailed 3D geometry of the porous electrodes.
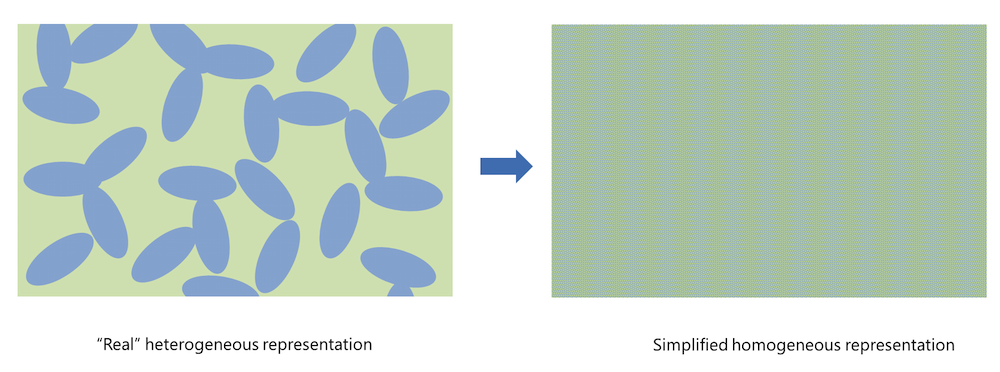
Figure 1. Homogenization simplifies the real heterogeneous porous electrode structure.
The Homogeneous Newman Model
Homogenization implies that the real porous structure is approximated with a slab, treated as a perfectly mixed solution of the solid particles (shown in blue in the figure above, to the left) and the pore electrolyte (shown in green). A consequence of the homogeneous representation is that the pore electrolyte (ion conductor) and the conducting electrode particles (electron conductor) are defined in the same geometrical domain. The effective charge and mass transport properties are then described using variables such as porosity and tortuosity to account for the observable effects of the specific geometry of the porous structure and the particles.
In a homogeneous porous electrode model, the charge transfer reactions that transfer the current between the electrode material and the pore electrolyte are introduced as balanced current sources and sinks for the electrode and electrolyte regions, in a similar fashion to the definition of a homogeneous reaction between two chemical species in a solution. A cathodic charge transfer reaction is a source in the balance of current for the electronic conductor, while it is the corresponding sink for the balance of current for the pore electrolyte. The material balances contain the corresponding sources and sinks, from Faraday’s laws according to the stoichiometry of the homogenized charge transfer reactions.
These types of porous electrode models have served well in the modeling and simulation of porous electrodes within many different types of electrochemical cells. But how valid are these models for describing the detailed design of the porous structure for the lithium-ion battery? Tommy Zavalis (a battery expert, former colleague, and current COMSOL customer) and I discussed this question during one of our “sacred” Swedish coffee breaks. Our conclusion was that we could not know the answer to that question until we compared a homogeneous model with a heterogeneous model. So, we built a heterogeneous model to validate the Newman model for an idealized 3D porous electrode geometry.
Building a Heterogeneous Model
In a heterogeneous model, the electronically conducting particles and the pore electrolyte are described explicitly in 3D, treated as two separate domains within the modeling space.
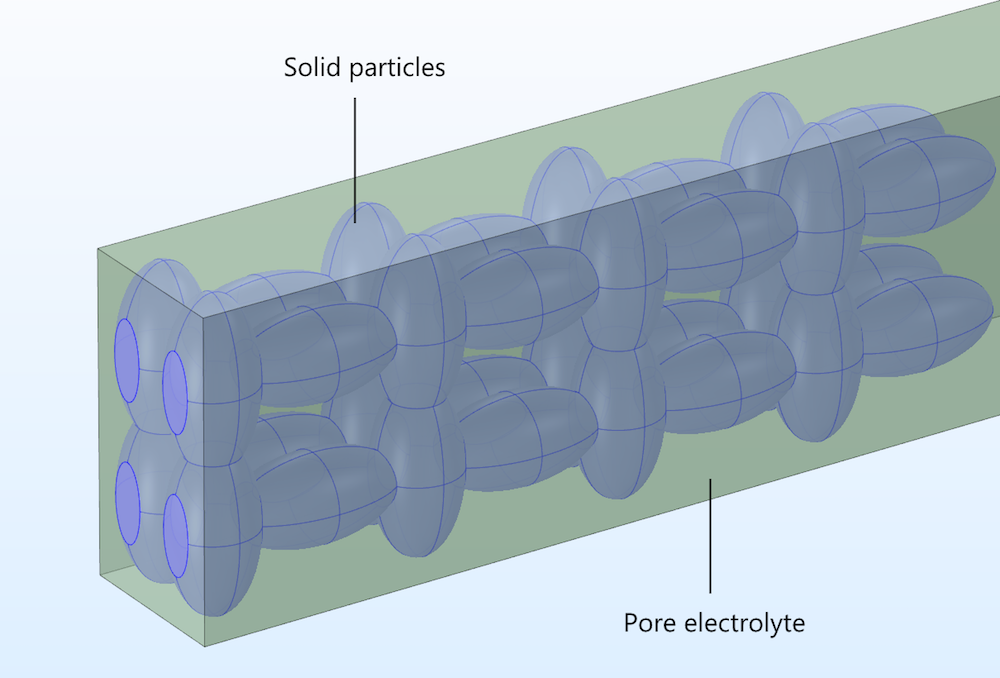
Figure 2. The pore electrolyte and particle domains in our idealized porous structure.
Current conservation for the ionic conductor is only defined in the pore electrolyte domain, while the current conservation for the conducting particles is only defined in the solid electrode domain. Mass transport of the ions is only defined in the pore electrolyte domain, with the surfaces of the solid particles forming the boundaries at which ions or other solution species can react by heterogeneous electron transfer. This contrasts with the homogeneous model, where the material balances and reactions are defined throughout a homogenized electrode domain.
Lithium metal formed at the surface of the solid particles is modeled as diffusing only in the particle domain itself, with the particle surface as the external boundary.
Evaluating the Accuracy of the Newman Model
Now, we can compare how well the Newman model and a heterogeneous model describe a detailed 3D structure. As a simple modeling experiment, we build an idealized unit cell with an idealized 3D porous structure, which we use for the negative and positive electrodes in a lithium-ion battery. The geometry is shown in the figure below, including streamlines to illustrate the current flow in the free electrolyte and the pore electrolyte. The electrode particles consist of ellipsoids that are rotated with the major axis in different directions in order to form a matrix of electron conductors, with the pore electrolyte contained in the void between particles.
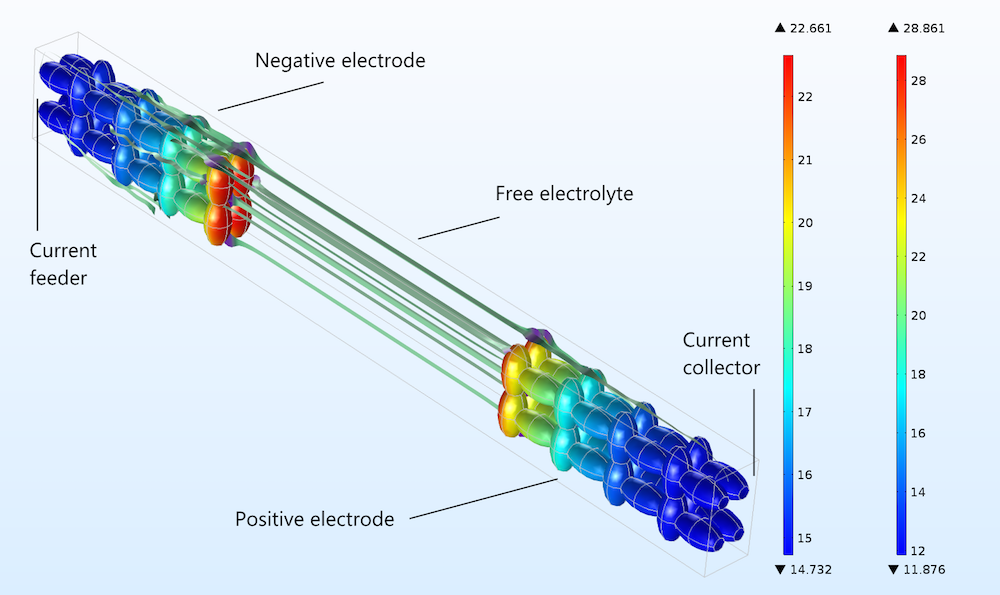
Figure 3. The charge transfer current density (A/m2) distribution in the positive electrode, shown in the geometry and color legend to the right, and the negative electrode, shown in the geometry and color legend to the left.
The figure above shows the absolute value of the charge transfer current density at the surface of the solid particles during discharge. The plot shows that the sides of the electrodes facing the current collector and feeder are less utilized than the sides facing the free electrolyte (or separator) between the electrodes.
We can change the rotation of the particles to create two different porosity distributions along the depth of the electrode, retaining a constant overall void-solid ratio (porosity). The results from the Newman model would not change under such a variation, since it only uses a universal average porosity as input.
Rotating the electrodes in Figure 3 by 180°, as indicated in the figure below for the positive electrode, gives a difference in current density distribution, but this difference is very small (shown by comparing the color legends of the two figures). Such a small difference in current distribution cannot even be detected with electrochemical impedance spectroscopy, as we’ll discuss below.
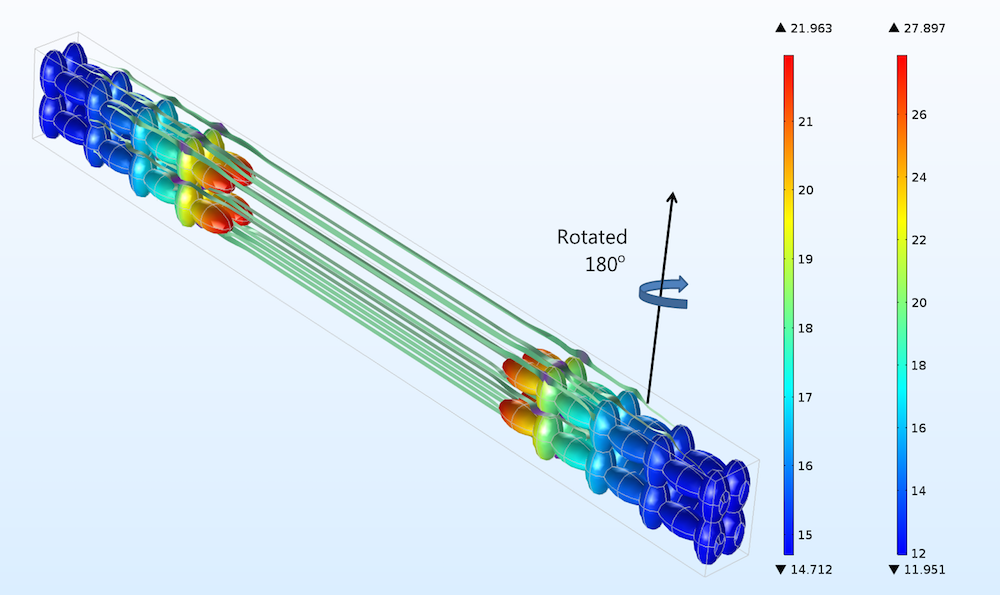
Figure 4. The positive electrode, right, and negative electrode, left, for the case when both the positive and negative electrodes have been rotated 180° in a horizontal plane. Compare to Figure 3 (only the rotation of the positive electrode is hinted above).
During our discussion over coffee, Tommy and I speculated that a method like electrochemical impedance spectroscopy (EIS), which separates subprocesses in the electrode with different time scales, would be able to catch the differences between different geometries. We therefore chose to simulate an EIS experiment for both the heterogeneous geometries and homogeneous Newman model.
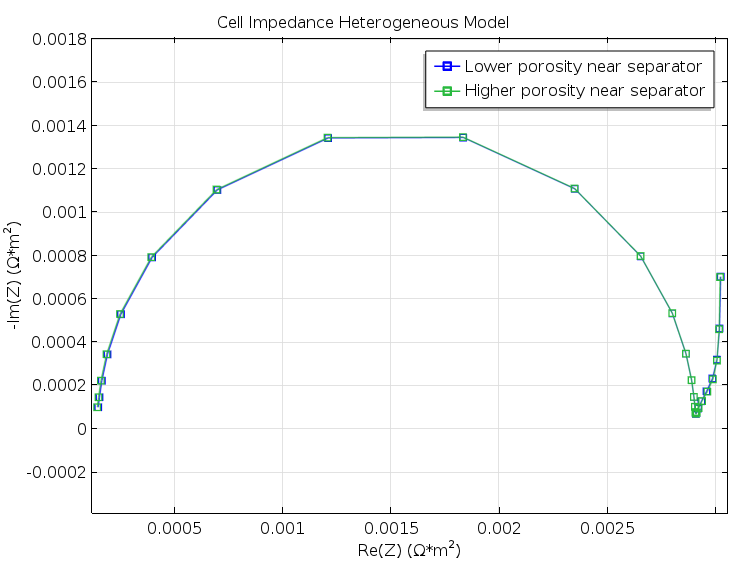
Figure 5. A Nyquist plot for the two model geometries in Figure 3 and Figure 4. The difference is very small and would not have been detected in a real experiment.
The results were both encouraging and disappointing. They are disappointing because the small change in structure for the cases in Figure 3 and Figure 4 does not show up in the Nyquist plots from the modeling experiments of the two geometries, as shown in Figure 5. The results are encouraging, however, because the Newman model gives a decent agreement with the heterogeneous model without any fitting whatsoever; see the figure below. This is somewhat surprising, since our idealized structure seems to be too coarse in its details to be effectively homogenized. For instance, the particle size is just one order of magnitude smaller than the width of the modeled unit cell.
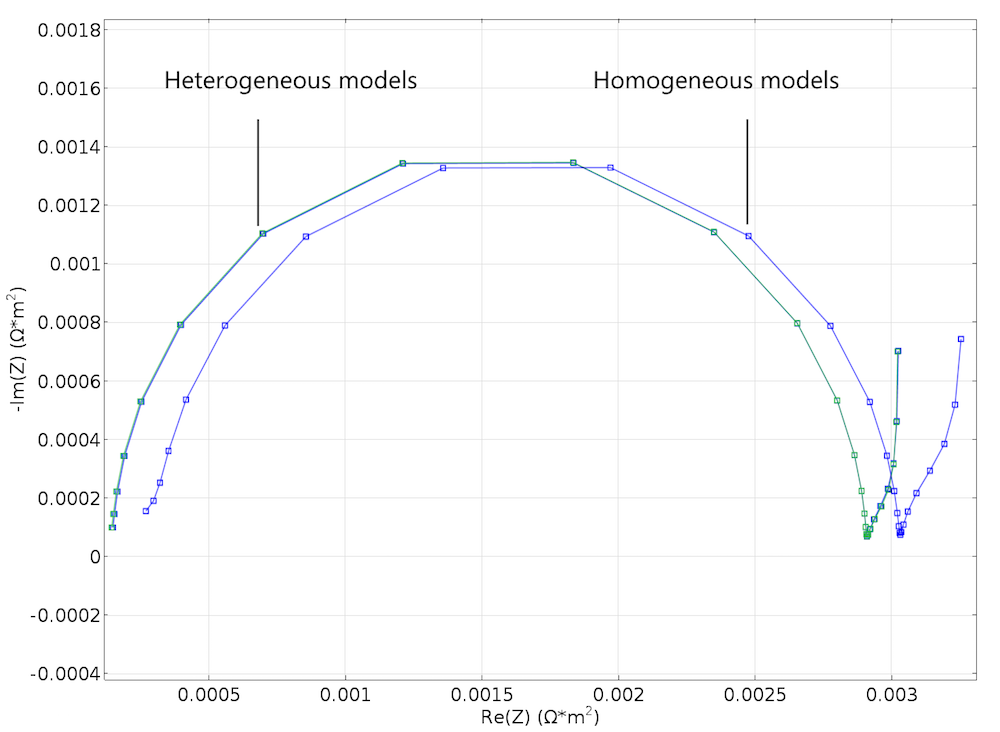
Figure 6. A Nyquist plot created by using the Newman model to simulate an EIS experiment. It is in good agreement with the corresponding plot for the heterogeneous model in Figure 5.
Concluding Thoughts on Modeling Li-Ion Batteries with Newman and Heterogeneous Models
Of course, the last word in this matter has not been said yet! We simulated a very simple structure, and the variations of the structure that we obtain by rotating the electrodes are clearly too small to impact the results dramatically. The natural next step is to try larger variations in the detailed description under constant averaged properties. Then, there is a chance that we can get a difference in the results in different heterogeneous structures, which would not be captured by the homogeneous Newman model.
Want to try it yourself? In the link below, you will find a short presentation of the models featured in this blog post, together with the COMSOL Multiphysics files that we used to produce the results above. You can make larger variations in the geometry or create your own geometry from scratch by using our models as a starting point.
For further reading, also check out these publications:
- J. O’M. Bockris and A. K. N. Reddy, Modern Electrochemistry Volume 2, Springer-Verlag, 1970.
- J. Newman and K. E. Thomas-Alyea, Electrochemical Systems 3rd Edition, Wiley, 2004.




Comments (2)
Kudakwashe Chayambuka
March 10, 2017Interesting read. isn’t an advantage of the homogenized model that it is relatively less computationally expensive since it can even be calculated in 1D or Pseudo-2D?
Caty Fairclough
March 22, 2017Hi Kudakwashe,
Thanks for your comment. The heterogeneous model is incredibly computationally intensive for all cases.
The homogeneous model is relatively inexpensive even for 3D cases. However, the homogeneous model equations can be somewhat expensive to solve for a 3D spiral cell or prismatic cell geometries.
So, the heterogeneous model can, in practice, only be used for very small unit cells to make really detailed studies regarding a cell’s microstructure. In such cases, the fidelity in the influence of the geometric description is difficult to match with a homogeneous model.
Best,
Caty