
Bicycle pedals stay on because the thread of the left pedal axle is left handed, while the right axle is right handed. The bearing torque works to unscrew the pedals, so the pedals stay on because there is a stronger effect involved; namely, the effect of mechanical precession. In this blog post, we will explain mechanical precession and demonstrate it on a bicycle model that involves a contact analysis and multibody dynamics.
A Peculiarity Noticed by Technical Cyclists
Whether you are new to riding or have been an avid cyclist since you could walk, you might have noticed something odd about the way a bicycle’s pedals are set up. The left pedal of a bike has left-handed threads and the right pedal has right-handed threads.

This observance has inspired many people to wonder why the pedals, threaded in their own direction on each side, don’t fall off after a certain amount of riding.
A further question comes from this one if you’ve ever had to do some of your own bicycle repairs: Which way do you turn each pedal to unscrew it?
What Is Mechanical Precession?
Mechanical precession occurs whenever a bolt is subjected to a force spinning around the bolt axis. The rotating force will cause the bolt to rotate in the opposite direction of the force dynamics. The animation below illustrates this basic principle.
A bolt (inner circle) is subjected to a force (black arrow) that is rotating counter clockwise. This causes the bolt to rotate clockwise (gray arrow).
This simplified 2D animation assumes a rigid bolt with a thread tolerance of 10%, which causes the bolt to rotate 36° for each revolution of the force. In practice, the tolerance is much smaller, the bolt is elastic, and there are large force variations in the out-of-plane dimension.
Try a simple mechanical precession trick for yourself right now: Hold a pen loosely in your hand, while moving the tip of the pen in a circle with your other hand. This will cause the pen to twist in the opposite direction of the rotation.
Multibody Dynamics with Contact Analysis of Bicycle Pedals
The basic principle can be captured by modeling only the bolt, the force on the bolt, and the crank arm in which the bolt is mounted. Such an animation would occur in a rotating frame, and it is difficult to verify the correctness of the imposed force dynamics.
Instead, we can build a multibody dynamics model in which the entire bike is considered. If only the bolt axle is considered elastic, the multibody dynamics model adds a negligible computational cost, and it allows for visualization of the force dynamics in a fixed frame.
When a bike is pedaled with clip-ons, there are both downward and upward forces on the pedal. A model simulating the complete bicycle will reveal that this causes the force to move in a half circle twice for each rotation of the pedals, as illustrated in the animation below.
The animation shows how the pedaling of a bike causes a clockwise rotation of the right pedal axle, when seen from the right side in the frame rotating with the axle. The rotating colors at the end of the bolt illustrate the contact pressure on a logarithmic scale.
It is critical that the contact analysis uses friction, so the model assumes a friction coefficient of 0.1.
The model also assumes a negligible thread tolerance and a realistic stiffness of the bolt axle. Realistic values of the force cause very small rotations due to mechanical precession, so for visualization purposes, the peak force is 50 kN, which is 50–500 times larger than realistic values. This is obvious when looking at the bolt deformation in the above animation. Even though the force is large, the precession is only around 1° per pedal rotation as shown in the below figure.
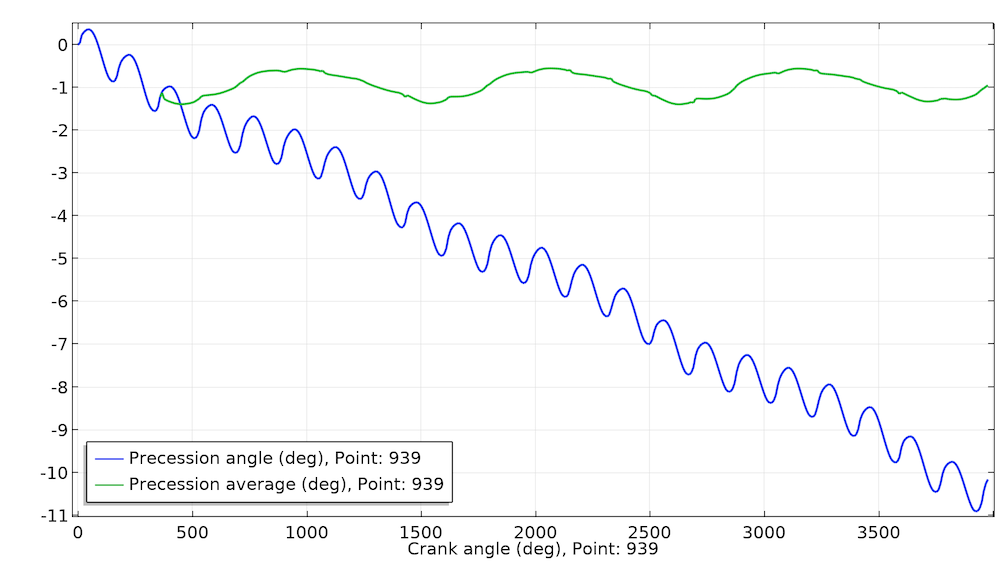
The angle of the bolt in the crank frame is shown in blue, while the value of this angle relative to the previous revolution is shown in green. The fluctuations in the green curve are due to numerical noise. The average value of the green curve is 0.95°.
What If You Need to Unscrew a Pedal on Your Bike?
If you ever need to unscrew a pedal, you can remember that:
- The phrase “righty-tighty and lefty-loosey” applies on the right side only
- The bearing force unscrews the bolt, so you can grip the bolt with a spanner and use it to “pedal” the bike forward
- Mechanical precession screws the bolt in, so you can switch to a fixed-gear setup and pedal the bike backward for an extended period of time (not recommended)
Try It Yourself
The model featured here uses the Multibody Dynamics interface, which supports the computation of deformation in different frames — simplifying the creation of animations in different frames. This functionality is new as of COMSOL Multiphysics® version 5.5.
Try performing a multibody dynamics study and contact analysis of the pedals of a bicycle yourself. Get the model by clicking the button below.




Comments (0)