
A question that comes up occasionally is whether or not you can compute the inductance of a single straight wire. This seemingly simple question actually does not really have an answer, and gives us the opportunity to talk about a very interesting point when solving Maxwell’s equations. Anybody working in the field of computational electromagnetics should have an understanding of this key concept, as it will help you properly set up and interpret models involving magnetic fields.
What is the Inductance of a Single Straight Wire?
Before we get to this concept, let’s look at the question again: What is the inductance of a single straight wire? To begin to address this, we consider the energy-based definition of inductance:
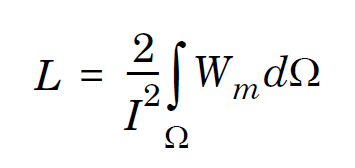
The inductance, L, is defined in terms of the current, I, flowing through the system, and Wm, the magnetic energy density is proportional to B2. The magnetic field, B, exists within and outside of the wire. Within the wire, it increases linearly outwards from the centerline, and outside of the wire it falls off as 1/r, where r is the radius. So, to compute the magnetic field and the magnetic energy distributions we build a model based on Maxwell’s equations, in this case Ampère’s Law. A current source is applied to one end of the wire while the other end is grounded. The normal component of the magnetic flux density is constrained to zero on the exterior boundaries of the model.
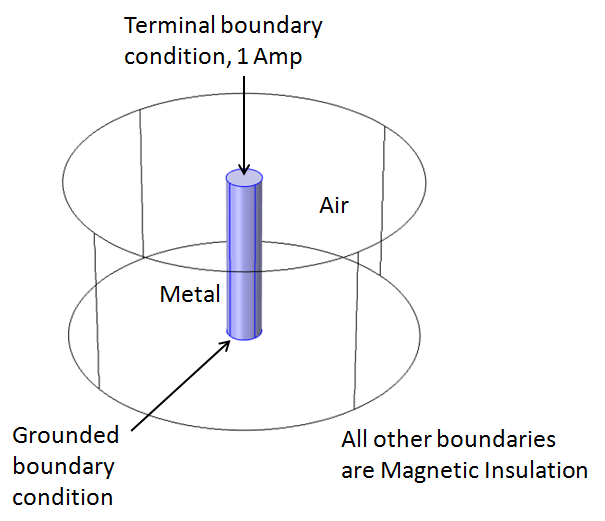
We can build this model in COMSOL Multiphysics using the Magnetic and Electric Fields physics interface of the AC/DC Module, which will solve for the electric fields and currents in the wire, as well as the magnetic fields in the wire and surrounding air. The Terminal boundary condition will excite the structure, and automatically compute the inductance using the above formula. The Ground boundary condition at the other end of the wire provides a current sink, and the Magnetic Insulation boundary condition sets the normal component of the magnetic flux density to zero.
Now, the fields extend infinitely around the wire, but the magnetic energy density falls off as 1/r2, so we might think that it is sufficient to study increasing radii of our modeling domain, and that the inductance will converge. If we try this, however, the inductance as a function of radius will look like this:
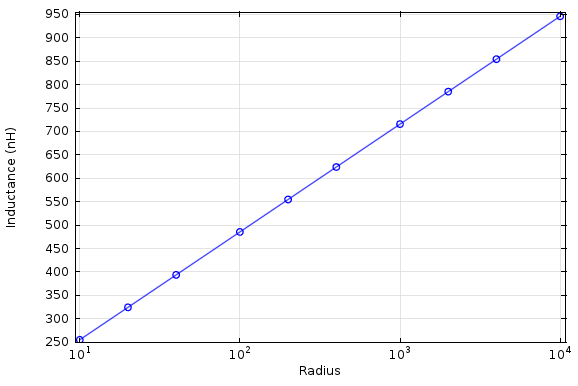
As the radius increases, the inductance also increases. No matter how large we make the modeling domain, the inductance for this model of a straight wire does not converge!
Not Only Solving for the Inductance
Things are looking rather grim if we can’t even compute this simple case correctly, right? Well, actually, we aren’t just solving for the inductance of the wire in this model. You are always solving for the inductance of the system, and that has to include the current return path. The governing Maxwell’s equations are formulated under the assumption that current (electrons) can be neither created nor destroyed. In fact, the Magnetic Insulation boundary conditions provide this current return path. We can see this by plotting the current in the volumes as well as the surface currents:
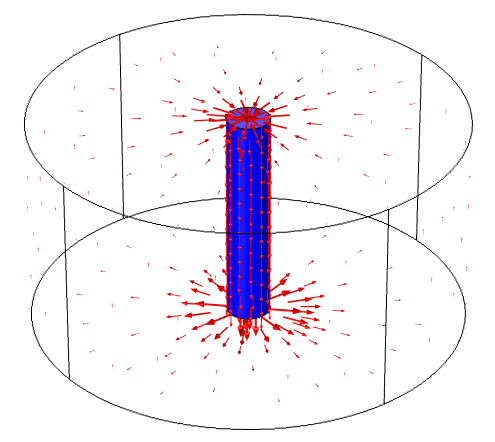
The red arrows in the figure above show that the current is flowing along the wire, and also flowing along the Magnetic Insulation boundary conditions as a surface current. The Magnetic Insulation boundary condition can be thought of as representing a material with infinite conductivity along which current can flow unimpeded. The current path in the above figure is solenoidal, meaning the current is flowing in a closed path. There is a conductive path not only from the terminal to ground boundary conditions, through the wire, but also from the ground boundary condition back to the terminals, along the boundaries.
Solenoidal Path
This concept of a solenoidal path for the current is the key point here. Whenever you are setting up any kind of magnetic fields model, you must ensure that current can flow in a closed loop. You don’t have a choice: this is required by Maxwell’s equations. You also have to be aware that this current return path will affect the results. In the above model, we are not only computing the inductance due to the current flowing along the wire, we are also considering the effect of the current flowing back along the magnetic insulation boundary conditions.
When setting up any kind of magnetic fields model, you have to model a complete solenoidal current path, and the inductance that you compute from such a model is of the entire current loop.
So that is why you can’t compute the inductance of a single straight wire!
Of course, as long as the system you are analyzing is solenoidal, with current flowing in a loop, you can correctly compute the inductance.
Further Reading
To see examples that compute the mutual inductance between circular loops of wire and compares against analytic solutions, please see:







Comments (10)
Ivar Kjelberg
May 14, 2013Well, so lets consider this as a closed loop then: hence similar to a coax induction line (per meter assumed “long”):
L = mu_r*mu_0*length/(2*pi)*ln(Rext/Rint) (H)
since both Rint and Rext are known when we design our cylinder.
and then compare this also to the known inductance of an “INF” straight conductor
L = mu_r*mu_0*length/(2*pi)*(ln(2*length/R)-3/4) (H) (approximation, ignoring cap effect)
And by normalising Wm, by using Rext, one can easily see the effect of the two cylinder caps, or even attempt the exercice by surrounding the straight inductor by a sphere instead of a cylnder 😉
Having fun Comsoling
Ivar
Walter Frei
May 14, 2013 COMSOL EmployeeYes, thank you Ivar, that’s a good point. The issue is really independent of the shape of the surrounding geometry.
Lingling Tang
July 17, 2013Dear Frei,
I simulated your problem about inductance of a wire,and actually the surface current density on the boundary flows from the ground to the terminal to form a loop circuit.
My question is if you plot the surface current density in the tutorial model “integrated square-shaped spiral inductor”,there will be also the so called loop, because the spiral inductor model is almost the same to your wire model,except a little geometry difference. So, does it also mean the spiral inductor’s inductance will also change if the dimensions of the outer air domain is changed?
What’s more, I didn’t try to test the relationship between the radii and convergence.
Walter Frei
July 17, 2013 COMSOL EmployeeYes Lingling, that is correct: The same observation can be made for any geometry, such as the “integrated square-shaped spiral inductor”. The assumption with that model is that there is a square metallic packaging of fixed size enclosing the device which provides the current return path.
Susant Patra
April 9, 2018Hi Walter,
How do you apply terminal boundary condition in mef module. I could not find the terminal option. Any pointer will be greatly appreciated.
Regards,
Susant
Caty Fairclough
April 26, 2018Hi Susant,
Thank you for your comment.
For your question, I would suggest contacting our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
Matt McCready
July 20, 2018I tried to build this simulation and others like it with the same boundary conditions, but I keep getting singular matrices and it fails to find a solution. Any ideas?
Caty Fairclough
August 7, 2018Hi Matt,
Thanks for your question!
In this case, I would suggest contacting our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
sreedhar srisailam
March 30, 2021Hi,
I would like to request the simulation file of “Computing the Inductance of a Straight Wire”.
Kindly help me in this regard, please.
Thank you in advance.
Rishabh Upadhyay
April 16, 2021Hi,
Can I please get a link to the .mph file of the topic of this blog (computing the Inductance of a Straight Wire)? I want to simulate a similar design BUT with curved wire forming meanders (without forming a loop). Thanks in advance.