Equation-Based Modeling Blog Posts

Introduction to Modeling Soap Films and Other Variational Problems
In this introduction to a 5-part series, learn how to solve variational problems using equation-based modeling, which is useful for modeling soap films, catenary cables, light beams, and more.

Chasing Waves: The Story of John Scott Russell and the KdV Equation
It all started with a horse: Learn about the history and use cases for solitons, as well as the life and work of the naval architect behind the KdV equation: John Scott Russell.

Acoustic Topology Optimization with Thermoviscous Losses
A guest blogger from GN Hearing discusses including thermoviscous losses in the topology optimization of microacoustic devices, such as hearing aids, mobile phones, and metamaterial geometries.

Predicting Solute Transport in Groundwater Using Simulation
In order for groundwater to be useful for irrigation and drinking, we need to understand how its various solutes move through the water. The Subsurface Flow Module includes features for this.

3 Examples of Equation-Based Modeling in COMSOL Multiphysics®
What are the benefits of using equation-based modeling in your simulations? Here are 3 examples that demonstrate the use of this functionality.

How to Generate Randomized Inhomogeneous Material Data
Did you know there is a way to take randomized material data with specified statistical properties determined by a spectral density distribution and use it to generate and visualize results?

How to Generate Random Surfaces in COMSOL Multiphysics®
Get a comprehensive background and step-by-step guide to generating random surfaces in COMSOL Multiphysics®, such as rough surfaces and microstructures.

Exploiting Maximum Principles to Save Time and Resources
By exploiting maximum principles in large and complex models, you will save time and computational resources without having to buy a bigger computer or leave your model to solve overnight.
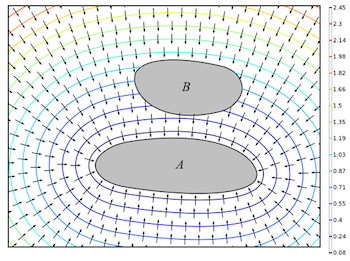
How to Compute Distances Between Objects in COMSOL Multiphysics®
Compute the distance between two deforming objects in the COMSOL Multiphysics® software. Here’s how…

Solving Shallow Water Equations with Equation-Based Modeling
Shallow water equations are an example of equation-based modeling. You can define expressions in COMSOL Multiphysics® to solve a shallow water equation for coastal erosion analyses.
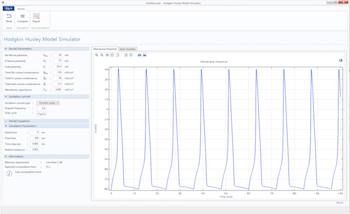
Analyze the Hodgkin-Huxley Model with a Computational App
The Hodgkin-Huxley model is an advanced model for simulating action potential. We also go over how to use a computational app to streamline this type of analysis.

Understand the Dynamics of the FitzHugh-Nagumo Model with an App
In 1961, R. Fitzhugh and J. Nagumo proposed a model for emulating the current signal observed in a living organism’s excitable cells. This became known as the FitzHugh–Nagumo model.
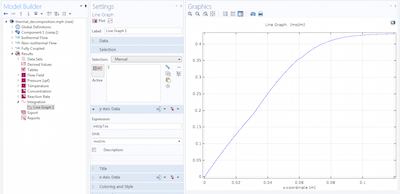
Integrals with Moving Limits and Solving Integro-Differential Equations
Learn how to analyze spatial integrals over variable limits, whether they are prescribed explicitly or defined implicitly. (Part 2 of 2)
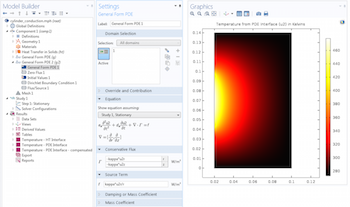
Guidelines for Equation-Based Modeling in Axisymmetric Components
Here’s your comprehensive guide to equation-based modeling for problems with cylindrical coordinates and axisymmetric components.

Investigating Turing’s Theory of Morphogenesis
Ever wonder how a tiger gets its stripes? Alan Turing’s theory of morphogenesis explains how patterns, such as stripes, develop naturally from initially homogeneous states.
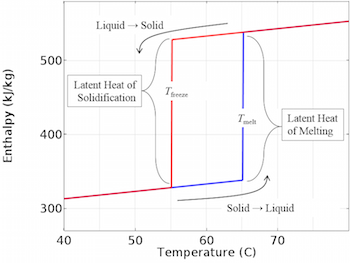
Thermal Modeling of Phase-Change Materials with Hysteresis
Hysteresis occurs when the melting temperature of a material is different from the solidification temperature. We demonstrate the thermal modeling of such a material here.

Modeling the Thermal Curing Process
Polymerization of a thermoset resin is one example of thermal curing, a process in which temperature-induced chemical change occurs in a material.
Analyze the Spread of Epidemic Diseases with Simulation
Did you know that public health officials use mathematical modeling techniques to study the flu and other infectious diseases to predict their spread and make informed decisions?
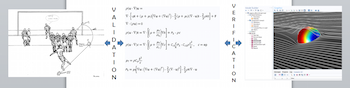
Verify Simulations with the Method of Manufactured Solutions
The Method of Manufactured Solutions involves assuming a solution, obtaining source terms, solving the problem, and comparing the results with the assumed solution. Use it to verify your models.
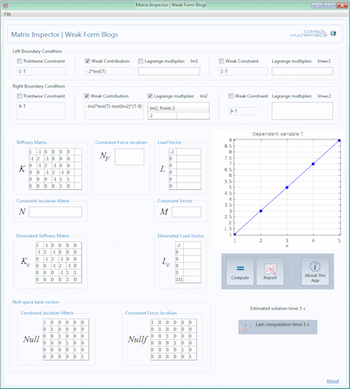
Implementing the Weak Form with a COMSOL App
First we implement the weak form equation and examine its matrices. Then we create a simulation app that displays all relevant matrices at once, arranged logically on one screen.
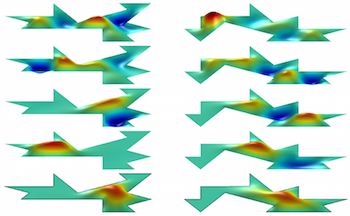
Can We Hear the Shape of a Drum?
Over half a century ago, Mark Kac gave an interesting lecture on a question that he had heard from Professor Bochner ten years earlier: “Can one hear the shape of a drum?”
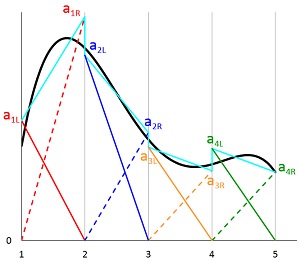
Discretizing the Weak Form Equations
In another installment of our blog series on the weak form equations, get an overview of how these equations are discretized and solved numerically in the COMSOL® software.
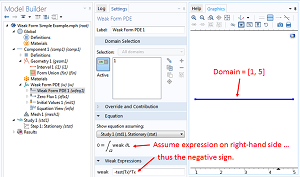
Implementing the Weak Form in COMSOL Multiphysics
In Part 2 of our series on the weak form equations, we demonstrate how to implement and solve these equations numerically using COMSOL Multiphysics®.
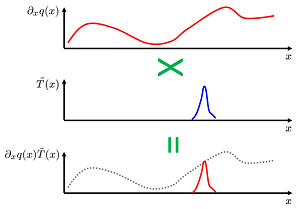
A Brief Introduction to the Weak Form
Whether or not you use finite element analysis and vector calculus in your daily life, you’ll appreciate this introduction to the weak form equations.
