All posts by Walter Frei
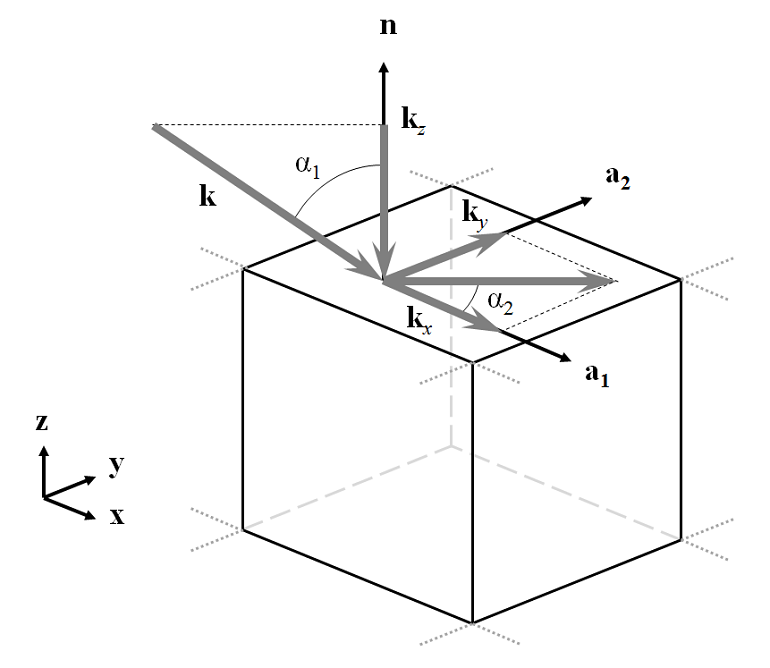
Modeling Electromagnetic Waves and Periodic Structures
Oftentimes, it is of interest to model an EM wave (light, microwaves) incident upon periodic structures, such as diffraction gratings, metamaterials, and frequency selective surfaces.
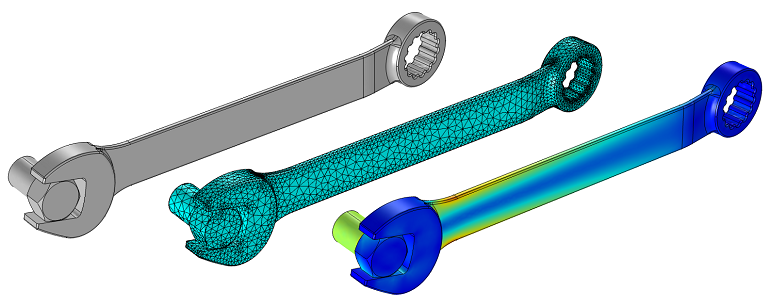
Parameterizing the Dimensions of Imported CAD Files
Learn how to modify an imported geometry with some clever usage of the Deformed Geometry interface in COMSOL Multiphysics®.
Using Adaptive Meshing for Local Solution Improvement
One of the perennial questions in finite element modeling is how to choose a mesh. We want a fine enough mesh to give accurate answers, but not too fine, as that would lead to an impractical solution time. As we’ve discussed previously, adaptive mesh refinement lets the software improve the mesh, and by default it will minimize the overall error in the model. However, we often are only interested in accurate results over some subset of the entire model space. […]
Learning to Solve Multiphysics Problems Effectively
One of the questions we get asked often is how to learn to solve multiphysics problems effectively. Over the last several weeks, I’ve been writing a series of blog posts addressing the core functionality of the COMSOL Multiphysics software. These posts are designed to give you an understanding of the key concepts behind developing accurate multiphysics models efficiently. Today, I’ll review the series as a whole.
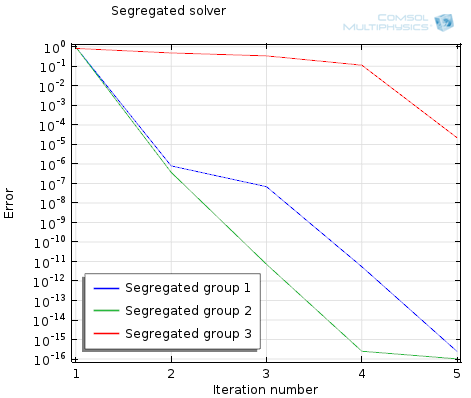
Improving Convergence of Multiphysics Problems
In our previous blog entry, we introduced the Fully Coupled and the Segregated algorithms used for solving steady-state multiphysics problems in COMSOL. Here, we will examine techniques for accelerating the convergence of these two methods.
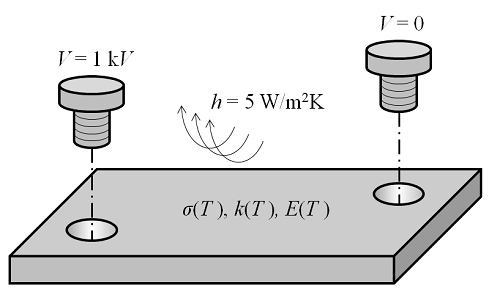
Solving Multiphysics Problems
Here we introduce the two classes of algorithms used to solve multiphysics finite element problems in COMSOL Multiphysics. So far, we’ve learned how to mesh and solve linear and nonlinear single-physics finite element problems, but have not yet considered what happens when there are multiple different interdependent physics being solved within the same domain.
Thermal Modeling of Surfaces with Wavelength-Dependent Emissivity
Whenever we are solving a thermal problem where radiation is significant, we need to know the emissivities of all of our surfaces. Emissivity is a measure of the ability of a surface to emit energy by radiation, and it can depend strongly upon the wavelength of the radiation. This is very relevant for thermal problems where the temperature variation is large or when there is exposure to a high-temperature source of radiation such as the sun. In this post on […]
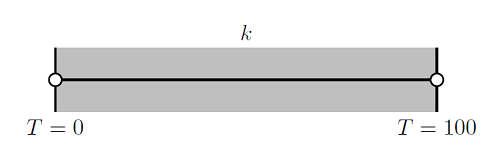
Meshing Considerations for Nonlinear Static Finite Element Problems
As part of our solver blog series we have discussed solving nonlinear static finite element problems, load ramping for improving convergence of nonlinear problems, and nonlinearity ramping for improving convergence of nonlinear problems. We have also introduced meshing considerations for linear static problems, as well as how to identify singularities and what to do about them when meshing. Building on these topics, we will now address how to prepare your mesh for efficiently solving nonlinear finite element problems.
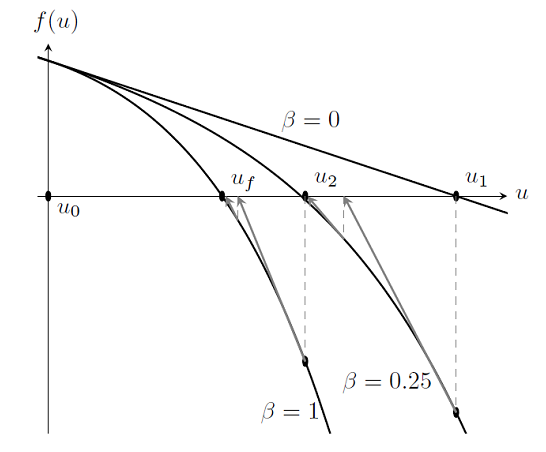
Nonlinearity Ramping for Improving Convergence of Nonlinear Problems
As we saw in “Load Ramping of Nonlinear Problems“, we can use the continuation method to ramp the loads on a problem up from an unloaded case where we know the solution. This algorithm was also useful for understanding what happens near a failure load. However, load ramping will not work in all cases, or may be inefficient. In this posting, we introduce the idea of ramping the nonlinearities in the problem to improve convergence.
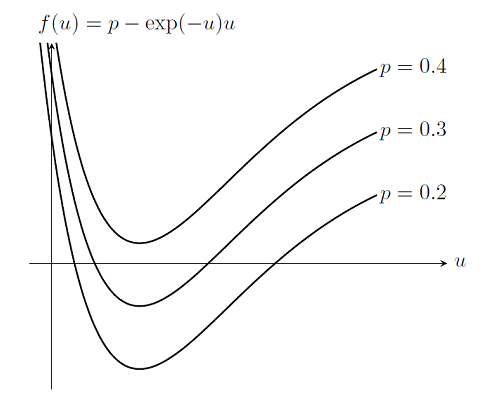
Load Ramping of Nonlinear Problems
As we saw previously in the blog entry on Solving Nonlinear Static Finite Element Problems, not all nonlinear problems will be solvable via the damped Newton-Raphson method. In particular, choosing an improper initial condition or setting up a problem without a solution will simply cause the nonlinear solver to continue iterating without converging. Here we introduce a more robust approach to solving nonlinear problems.
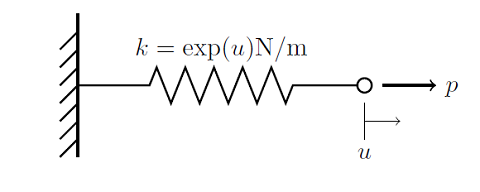
Solving Nonlinear Static Finite Element Problems
Here, we begin an overview of the algorithms used for solving nonlinear static finite element problems. This information is presented in the context of a very simple 1D finite element problem, and builds upon our previous entry on Solving Linear Static Finite Element Models.
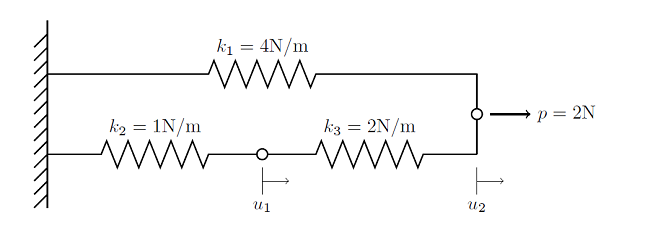
Solutions to Linear Systems of Equations: Direct and Iterative Solvers
In this blog post we introduce the two classes of algorithms that are used in COMSOL to solve systems of linear equations that arise when solving any finite element problem. This information is relevant both for understanding the inner workings of the solver and for understanding how memory requirements grow with problem size.
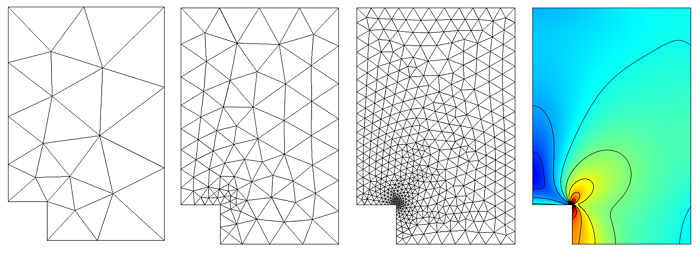
Meshing Your Geometry: When to Use the Various Element Types
In a previous blog entry, we introduced meshing considerations for linear static problems. One of the key concepts there was the idea of mesh convergence — as you refine the mesh, the solution will become more accurate. In this post, we will delve deeper into how to choose an appropriate mesh to start your mesh convergence studies for linear static finite element problems.
How to Identify and Resolve Singularities in the Model when Meshing
In our previous post on Meshing Considerations for Linear Static Problems, we found that, in the limit of mesh refinement, the solution to the finite element model would converge toward the true solution. We also saw that adaptive mesh refinement could be used to generate a mesh that would have smaller elements in regions where the error was higher, rather than simply using smaller elements everywhere in the model. In this post, we will examine a couple of common pitfalls […]
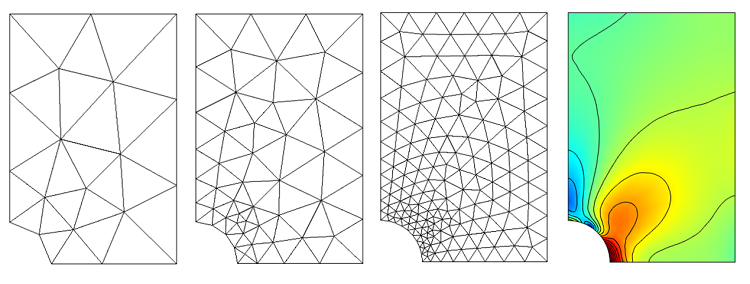
Meshing Considerations for Linear Static Problems
In this blog entry, we introduce meshing considerations for linear static finite element problems. This is the first in a series of postings on meshing techniques that is meant to provide guidance on how to approach the meshing of your finite element model with confidence.
Solving Linear Static Finite Element Models
In this first blog entry of our new solver series, we describe the algorithm used to solve all linear static finite element problems. This information is presented in the context of a very simple 1D finite element problem, but is applicable for all cases, and is important for understanding more complex nonlinear and multiphysics solution techniques to be discussed in upcoming blog posts.
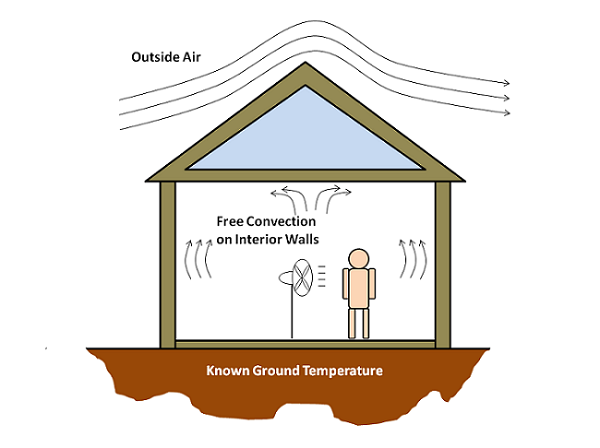
Using Global Equations: Modeling Room Air Temperature in a House
An interesting question came up the other day that I felt would make an excellent blog post since it allows us to discuss one of the very powerful, and often underutilized, features of COMSOL Multiphysics: the Global Equation. In this post, we will look at using global equations to introduce an additional degree of freedom to a model. This additional degree of freedom will represent something we do not want to model explicitly.
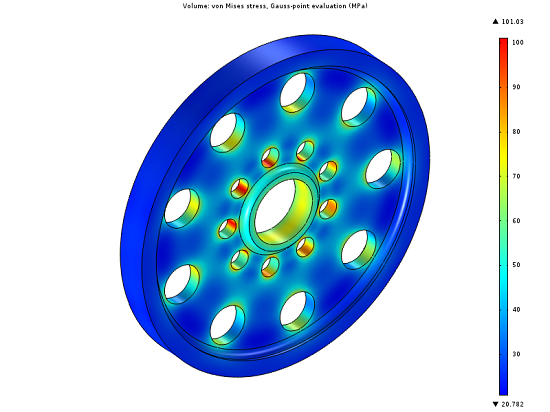
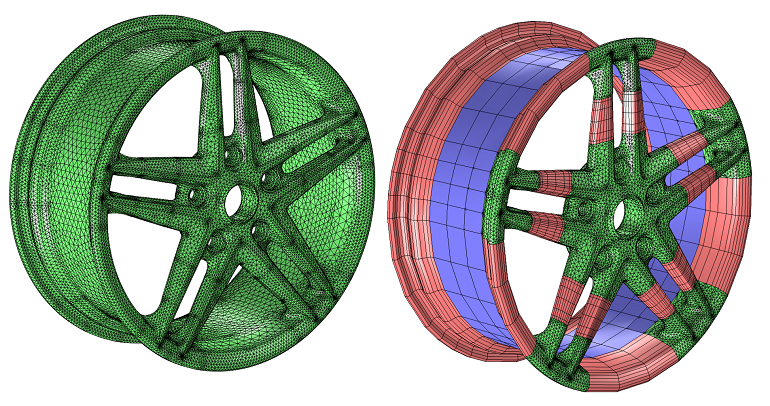
Using Gradient-Free Optimization
The COMSOL Optimization Module includes both gradient-based and gradient-free optimization techniques. Whereas the gradient-based optimization method can compute an exact analytic derivative of an objective function and any associated constraint functions, it does require these functions to be smooth and differentiable. In this blog post, we examine the use of the gradient-free optimizer, which can consider objective function and constraints that are not differentiable or smooth. The dimensions of a spinning wheel are optimized to reduce the mass while maintaining […]
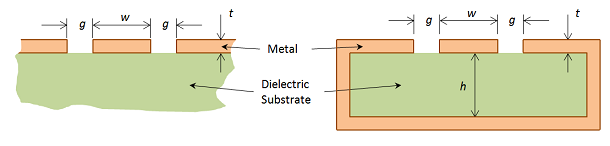
Modeling of Coplanar Waveguides
The Coplanar Waveguide (CPW) is commonly used in microwave circuits. COMSOL Multiphysics, with the RF Module, makes it easy to compute the impedance, fields, losses, and other operating parameters needed when designing a CPW.
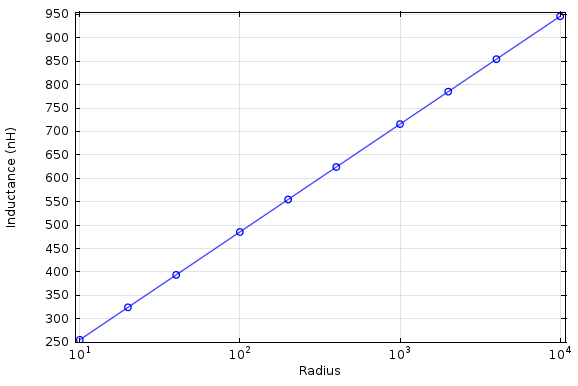
Computing the Inductance of a Straight Wire
A question that comes up occasionally is whether or not you can compute the inductance of a single straight wire. This seemingly simple question actually does not really have an answer, and gives us the opportunity to talk about a very interesting point when solving Maxwell’s equations. Anybody working in the field of computational electromagnetics should have an understanding of this key concept, as it will help you properly set up and interpret models involving magnetic fields.
Using Point Cloud Data in Your COMSOL Model
There is sometimes a need to include data from other simulation packages into a COMSOL Multiphysics model. There are a variety of ways in which this can be done, but one of the easiest approaches is to read in the point cloud data via a spreadsheet format text file. In this blog post, we walk through the steps of reading in such data, and using it in a COMSOL model.