
Researchers from AltaSim Technologies presented a paper at last year’s COMSOL Conference in Boston sharing their analyses on Mie scattering of electromagnetic waves and how they compare to the Mie solution.
Scattering
Scattering is a process where forms of radiation (e.g., light) are redirected from their original path of propagation due to interaction with obstacles, such as molecules, particles, droplets, and bubbles to name a few. These obstacles can be referred to as scatterers, as they are responsible for the deviation of radiation that occurs during the scattering process.
Mie Scattering
Mie scattering is the scattering of electromagnetic waves caused by a sphere and is described by the Mie solution to Maxwell’s equations. During this process, an electromagnetic wave illuminates an obstacle (a spherical particle in this case) and excites electric charges in the particle due to an interaction with the incident wave’s electric field. The oscillating charge causes electromagnetic energy to radiate in all directions (this radiation is scattered by the obstacle.) Along with re-radiating electromagnetic energy, the excited charges can transform some of the incident energy into other forms, such as thermal energy, through absorption. The scattering and absorption that occur results in the attenuation, or extinction, of the electromagnetic wave as they remove energy from it.
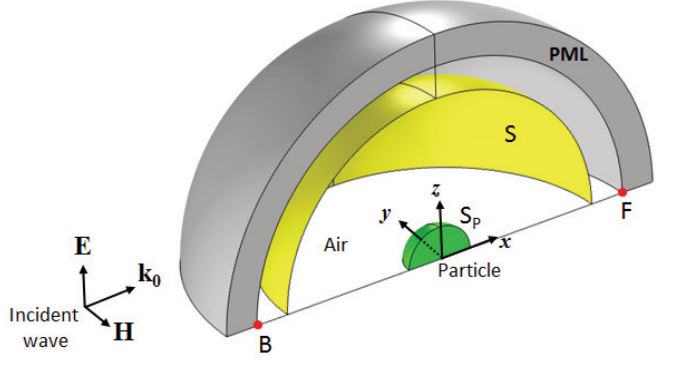
COMSOL Multiphysics model geometry for Mie scattering by a spherical particle. Model by S. Yushanov, J. Crompton, and K. Koppenhoefer. Image taken from their paper submission.
Modeling Mie Scattering of Electromagnetic Waves
AltaSim Technologies engineers Sergei Yushanov, Jeffrey S. Crompton, and Kyle C. Koppenhoefer analyzed this process with COMSOL Multiphysics. Then, they compared their findings with the Mie solution, documented their results, and presented them at the COMSOL Conference 2013 in Boston. Their analysis provides insight on the scattering, absorption, extinction, back-scattering, pressure cross sections, and radiation force exerted on the spherical particle by an incident plane wave. In the paper, they compared the results of their analyses against analytical solutions.
In their research, they considered particles with three different material properties — metallic, magnetic, and dielectric — all with a fixed radius and studied the nature of the interaction. They were able to calculate far-field variables with a built-in far-field node on the inner boundary of their model’s perfectly matched layer (PML) domain and calculate the total scattered energy.
Here are their results for the magnetic particle:
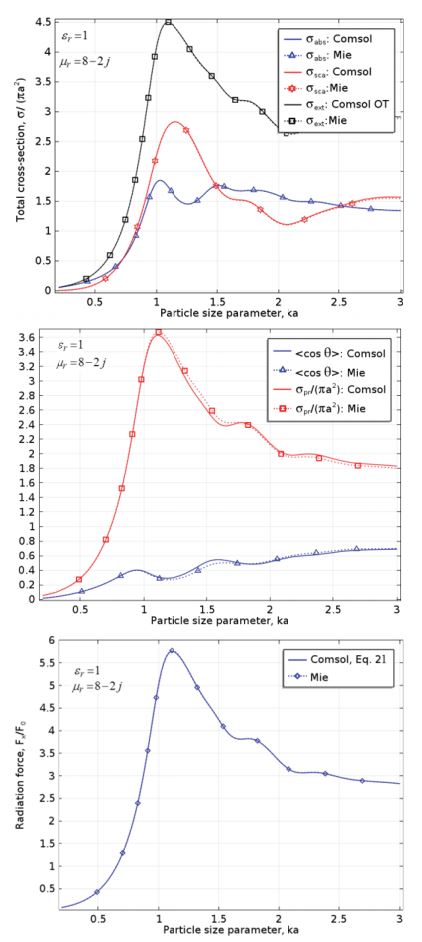
Cross section parameters and radiation force for the magnetic particle. Image by S. Yushanov, J. Crompton, and K. Koppenhoefer and taken from their paper submission.
When comparing their results to the Mie solution, they found that there was excellent agreement for cross sections and radiation force. (Note that the results assume only elastic scattering. Brillouin or Raman scattering are not included.)
Want to present your work like AltaSim Technologies did? You can, by submitting it for the annual COMSOL Conference.
Download the Paper and Presentation
- Check out the full paper and presentation: “Mie Scattering of Electromagnetic Waves“





Comments (7)
Jalpa Soni
March 10, 2015I have couple of question regarding this model, if i modified this model to find out the scattering cross section of the array of sphere. What is the procedure to find out the scattering cross section due to the whole array?
Kyle Koppenhoefer
March 10, 2015The scattering cross section of an array of spheres can be calculated using the same procedure as for a single sphere.
1. Calculate scattered energy by integration of the Poynting vector over an imaginary surface S around the array:
W_sca=intop1_S(-(emw.relPoavx*nx+ emw.relPoavy*ny+ emw.relPoavz*nz)) [W]
2. Calculate incident irradiance, defined as energy flux of the incident (background) wave:
P0=c0*epsilon*E0^2/2, [W/m^2]
where c0 is speed of light, epsilon is permittivity, E0 is background incident plane wave amplitude
3. Calculate scattering cross section:
sig_sca=W_sca/P0 [m^2]
Jalpa Soni
March 10, 2015Hello Kyle..
Thanks for your suggestion..
I am doing the same thing that you had stated. My question is that when i am calculating the effect of array by introducing floquet boundary condition. Then in that case what would be my integration surface, is it be the surface of nanoparticle or any surface which lie in the the far field domain??
Kyle Koppenhoefer
March 11, 2015Hello Jalpa- Developing the solution for an array of particles using the Floquet boundary conditions produces a complex problem. I recommend that you direct that question to Comsol support for a detailed response.
mohammad qasim
March 24, 2016I want to reproduce these results, please tell me what is the range of frequency of incident light? And how can we transform the result from frequency to size parmeter???
Kyle Koppenhoefer
March 29, 2016For particle size of a=0.1um and particle size parameter range 0.2<ka<3, the frequency range is 9.5e13Hz<f<1.4e15Hz
Ahsan
April 26, 2020I want this model How i can get it? Kindly help me