
In many simulation tasks, it is necessary to transfer variables from one region of a computation domain (the source) to another region or component (the destination). In COMSOL Multiphysics, this functionality is achieved by defining a point-to-point map, called an extrusion operator, that relates a set of destination points with a set of source points. Once a mapping is established by an extrusion operator, all variables defined at the source can be accessed from the destination using the same operator.
Mapping Variables Between Regions
There are many practical situations in which mapping variables from one component, or part of a component, to another is needed. One instance is the linking of two submodels, for example, the generation of inlet boundary conditions for turbulent flow models. The boundary conditions at the inlets significantly affect the flow in the domain. However, the flow profiles at the inlets are not as easily defined as with laminar flow. To generate turbulent inlet boundary conditions, an auxiliary model with normal inflow can be used. The resulting velocity profile at the outlet then needs to be copied to the inlet of the main model.
Editor’s note on 3/9/23: This manual mapping between two components is no longer necessary to get fully developed flow profiles. COMSOL Multiphysics now includes a Fully developed flow option, which can be applied to Inlet and Outlet boundary conditions for laminar and turbulent flow. (To learn more check out the 5.3a and 5.4 release highlights.)
Efficiency can be another reason to map variables between regions. Consider thermal expansion with axisymmetric thermal boundary conditions and material properties. If the structural boundary conditions are not axisymmetric, we can save time by performing an axisymmetric thermal analysis first, and then mapping the temperature from the 2D axisymmetric domain to the 3D domain for structural analysis.
Another common scenario is the implementation of periodic or other boundary conditions where a quantity at a point on a boundary is related to a quantity at a point on another boundary. For example, in a diode, the normal current density on one side of the p-n junction depends on the electric potential at the same point and the electric potential on the other side of the junction. While a variety of such boundary conditions are built into the appropriate physics interfaces in COMSOL Multiphysics, from time to time users may need to construct their own.
Such instances require point-wise mapping of variables from one domain or boundary to another. Today, we will show how these mappings can be constructed.
Mapping Between Source and Destination
The idea of a mapping involves two geometric entities: the source where a quantity is known and the destination where the quantity will be used. We know a quantity, q_s, at the source and want to calculate another quantity, q_d, at the destination. The new quantity, q_d, can be a copy of q_s or a function of it.
We can break this problem down into these steps:
- Go to a point, x_d, where we want to evaluate q_d.
- Identify the source point, x_s, corresponding to x_d. Let this coordinate transformation be given by x_s = T(x_d).
- Extract q_s = q_s(x_s).
- Insert the value of q_s as an argument to a function f:q_s\rightarrow q_d to evaluate q_d.
We end up with
The focus of this blog post is on the transformation T : x_d \rightarrow x_s.
COMSOL Multiphysics offers two coupling operators to specify this mapping: Linear Extrusion operators and General Extrusion operators. Linear Extrusion operators are easier to build, but their utility is limited to affine transformations. General Extrusion operators are more general but take more work to define.
Here, we will discuss Linear Extrusion operators. In a later blog post, we will deal with General Extrusion operators.
Using Linear Extrusion Operators in COMSOL Multiphysics
When the source and destination points are related to each other by affine transformations such as translation, scaling, reflection, rotation, or shear, COMSOL Multiphysics provides a simple way of specifying the extrusion operator: the Linear Extrusion operator. To add a Linear Extrusion operator, we go to Definitions>Component Couplings>Linear Extrusion.
The basic idea of a Linear Extrusion operator is that an affine transformation between two lines can be defined if we know two corresponding pairs of points on the lines. Similarly, three pairs of noncollinear points and four pairs of nonplanar (with no more than two collinear) points are enough to describe affine mappings of 2D and 3D domains, respectively.
This is similar to linear system analysis in general. If we know the transformation of a sufficient number of base points/vectors, we can transform every point/vector using linear superposition. Think of the Linear Extrusion operator as a visual way of picking the basis and their transformations. From that information, COMSOL Multiphysics automatically derives the mapping that needs to be applied on an arbitrary point/vector.
We will illustrate this with a few examples.
Example 1
The first operator is used for mapping data from the line segment with ends 1 and 4 to the line segment with ends 4 and 5, with the orientation preserved. All we need to do is indicate to COMSOL Multiphysics which point goes where, as shown in the image below.
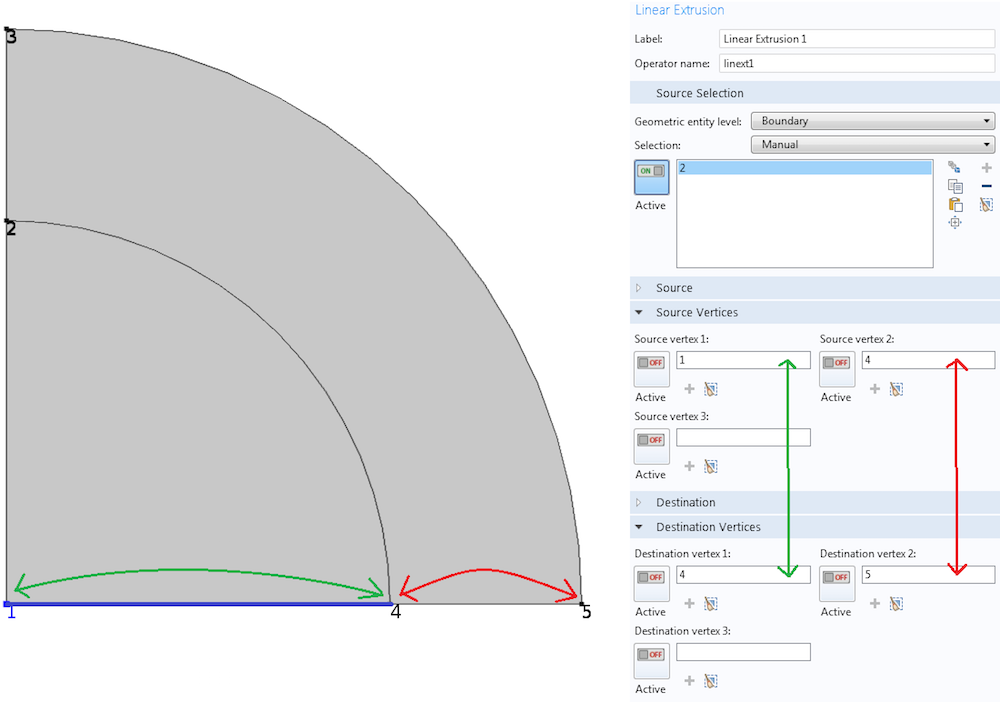
A Linear Extrusion operator matching points 1 and 4 in the source to points 4 and 5 in the destination, respectively.
Note that even though we are in a 2D space, we are working with 1D objects (lines). Thus, it suffices to indicate the correspondence between two sets of vertices. What if we choose 5 for Destination vertex 1 and 4 for Destination vertex 2? In that case, in addition to the translation and stretching needed to take segment 1-4 to segment 4-5, there will be a flipping. See the plot below.
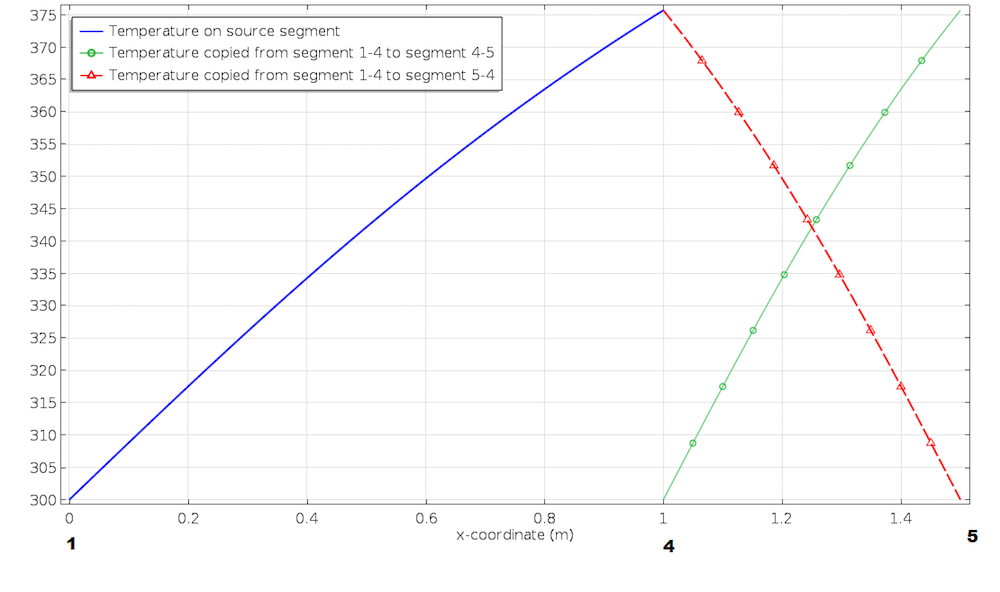
The order of vertices under Source Vertices and Destination Vertices of a Linear Extrusion operator determines the orientation of the mapping.
Example 2
Now, let’s increase the dimension of our objects and build the Linear Extrusion operator to copy data from the interior circle to the outer domain by radially stretching. All we need to do is to add one more pair of vertices to the above vertex pairing. See the Linear Extrusion settings window below.
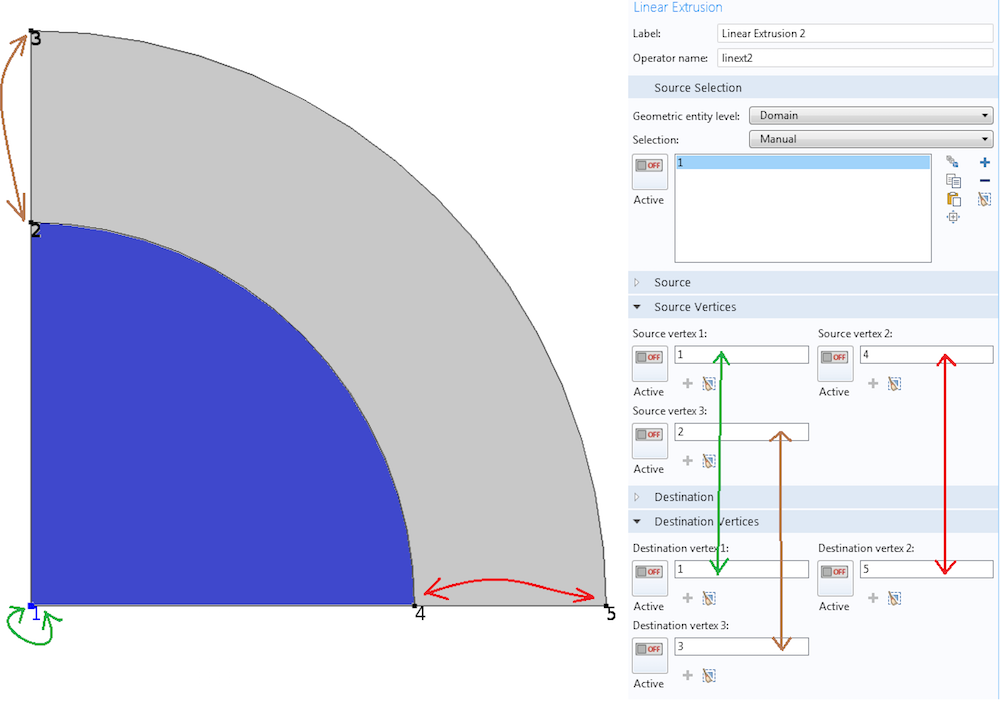
The higher the dimension of objects in the mapping, the more vertices in the geometry need to be paired up to define a Linear Extrusion operator.
The mapping matches points 1, 4, and 2 in the source domain to points 1, 5, and 3 in the destination domain, respectively. If we want to look at this in terms of basis vectors, segment 1-4 in the source corresponds to segment 1-5 in the destination. Similarly, segment 1-2 in the source corresponds to segment 1-3 in the destination. From these two linearly independent bases, COMSOL Multiphysics gets enough information to construct the mapping that takes any destination point in the 2D domain to a source point. The figure below shows how a variable \phi defined on the interior circle is mapped by the Linear Extrusion operator linext2 that we just defined.
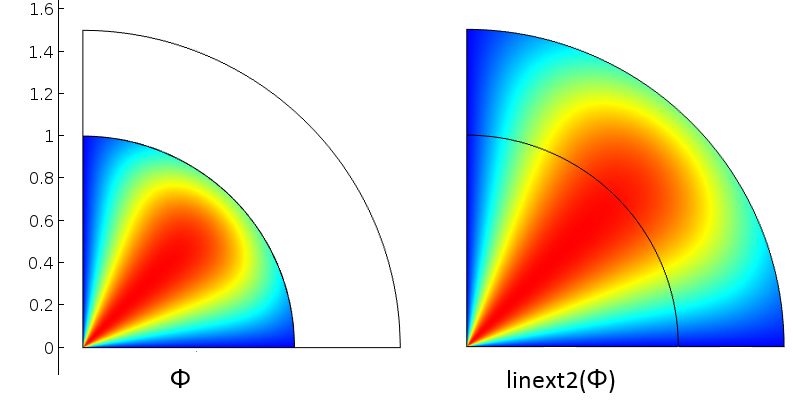
A variable defined over interior circle (left) and mapped to all points using the Linear Extrusion operator (right).
Evaluating Quantities
What we have done up to now is build the infrastructure that will help us access variables. Now, let’s see how to use the tool we built.
If we look at any of the Linear Extrusion settings windows shown in the images above, we see Operator name at the top. That name is what we will use to access the mapping. If linext2 was the name of the extrusion operator, any time we are at a destination point and want to refer to a quantity, say u, from the corresponding source point, we use the expression linext2(u). If we want the variable w from the same source point, we use linext2(w). This explains why we call them operators. Once we build them, we can use them with any legitimate argument.
Instead of just using a variable, if we want a function of the variable, we can put the function either inside the operator or apply the function to the output of the operator. For example, linext2(w^2) is equivalent to linext2(w)^2. Does linext2(w)+u return the same value as linext2(w+u)? Generally, no. In the first case, u at a destination point is added to w evaluated at the corresponding source point. In the second case, both u and w are evaluated at the source point. The image below illustrates this point using the Linear Extrusion operator from Example 2.
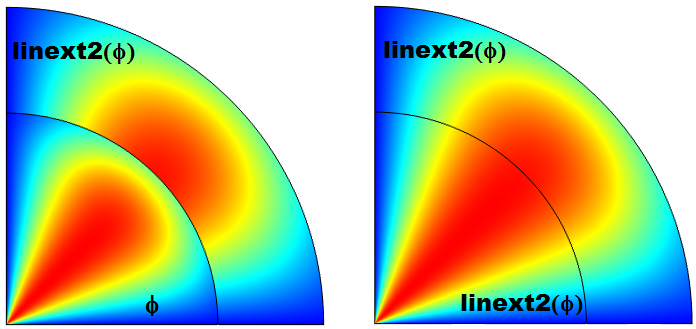
The variable \phi is evaluated at the destination in the inner circle and at the source in the outer arc (left). All evaluations are at the source (right). Note that in general, the argument, such as \phi, can be a valid quantity at a destination point. In such cases, its value is generally different from the value returned by the extrusion operator.
Finally, when using an extrusion operator to map variables between different components, the operator should be added to the Definitions node of the component containing the source object. That component’s tag should be used when we use the operator in another component. To access a variable u defined in component 1 from component 2 using the Linear Extrusion operator linext2, the correct syntax is comp1.linext2(comp1.u). This avoids confusion if there is an extrusion or another operator also called linext2 or another variable called u in the second component.
Closing Remarks
The focus of this blog post is the construction of Linear Extrusion operators. Check out Part 2 of this blog series on how to build General Extrusion operators, where we will illustrate their use in a full modeling example.




Comments (3)
Oana Tucaliuc
October 14, 2015Dear Temesgen,
This is a very useful blog but regarding Linear Extrusion operators, I noticed complete absence of their implementation for particle tracing. Consider two identical cylinders placed on the top of each other distributed in two 3D components of the same Comsol file such that they share a boundary (normal to their height and flow direction). One can study laminar flow setting the inlet into the lower cylinder to receive the flow velocity generated in the upper cylinder at its outlet. Furthermore particles can be traced along the upper cylinder but I donțt know how to transmit their coordinates in the lower cylinder. Something like comp1.linext1(comp1.qx) … would be needed but there appear two questions:
1) where can such information be written, inside the fpt physics? Neither Inlet nor Release from Grid seem to allow this.
2) Thinking that particles in the upper cylinder are generated with random diameter how can this information be transmitted to the lower cylinder. Is the particle index a useful quantity here, in the sense that an index can store position and diameter for each particle?
This kind of problem arises when working with large structures which are better handled by parts due to meshing problems and, to my knowledge, is not treated in any of the Comsol documents (user guide, blog, model gallery). If possible a blog on the subject would be highly appreciated.
Many thanks!
The subject is not treated in
Hugo Cabrera
December 12, 2015Dear Temesgen,
I have the same comment/problem about using extrusions in charged particle tracing.
Best regards,
Hugo Cabrera
Temesgen Kindo
December 14, 2015Dear Oana & Hugo,
Thank you for your comments and questions.
Please contact COMSOL Technical Support at support@comsol.com about this. A brief explanation of why you want to do that will help us understand your question better.
Thank you,
Temesgen