
Research on fatigue started in the 19th century, initiated following failing railroad axles that caused train accidents. In a rotating axle, stress varies from tension to compression and back to tension in one revolution. The load history is simple because it is uniaxial and proportional. Fatigue can then be evaluated with the S-N curve, also known as the Wöhler curve, which relates stress amplitude to a component’s life. In many applications we deal with multiaxiality and non-proportional loading. In this instance, the S-N curve is insufficient for fatigue prediction. Critical plane models examine stress state in different orientations in space and can therefore incorporate some effects of multiaxiality and non-proportionality. Because they can accurately predict the fatigue failure phenomena for many structural applications, they have gained a wide acceptance among the engineering community.
About Critical Plane Models
The idea behind critical plane models is that failure is caused by a crack. The crack will form and run on a plane, a critical plane, that has the most favorable stress/strain conditions for either crack growth, crack propagation, or both events. Planes that experience the highest normal stresses and strains are usually good candidates for a critical plane.
The stress state in a point in a structure can be described with a two-dimensional tensor with three normal and three shear components. The magnitude of those stresses changes once the examined volume element is oriented in a different direction. This means that if we make a cut through a volume element and evaluate stresses on the newly created plane, its stress state will change depending on the orientation. In case of plane stress conditions, the stress state reduces to two normal stresses and one shear stress that also differ depending on the surface normal.
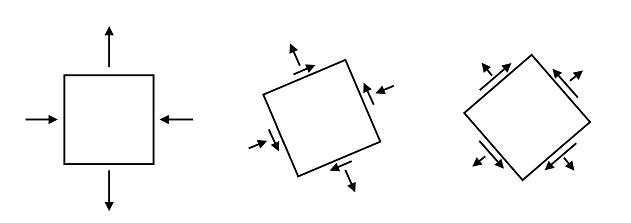
Stress conditions on different planes.
A plane in a volume element has one normal and two shear stress/strain components. A critical plane model utilizes those stress/strain components to define the critical plane in its own specific way. For example, the Normal stress criterion considers a plane with the largest normal stress range, the Findley model searches for a plane where the combination between the normal and the shear stress ranges is maximized, while the Matake criterion, on the other hand, evaluates planes with the highest strain range. From the picture above, it is clear that all of the planes have different orientations.
Fatigue Prediction Models
For plane stress conditions, the critical plane can be obtained with analytical expressions. The situation becomes more challenging when the load is non-proportional and the stress state is multiaxial. We must then search for the critical plane numerically and evaluate the load history in each examined plane orientation. This is done in the Fatigue Module with the Stress-based and the Strain-based models.

Fatigue evaluated with critical plane criteria: Normal stress, Findley, and Matake. Note from the editor, 2/24/14: This image has been updated with results from COMSOL Multiphysics version 4.4.
In the Stress-based models we can calculate Normal stress, Findley, and Matake criteria. These are evaluated according to the fail-safe philosophy — calculating the fatigue usage factor that determines whether the experienced fatigue load is above or below a fatigue limit. The material parameters for those models can be easily calculated from the results of standard fatigue tests. Stress-based models are usually used in the high-cycle fatigue domain where plasticity is very limited.
The Strain-based models evaluate strains or combination of strains and stresses when defining a critical plane. Those models can be seen as a modified, combined Basquin and Coffin-Manson strain-life relation. They predict the number of cycles to failure. In the Fatigue Module, there are three Strain-based models: Smith-Watson-Topper (SWT), Wang-Brown, and Fatemi-Socie. Those models are suitable for low-cycle fatigue where strains are usually large.
Fatigue Modeling Examples
I’d like to share three examples of fatigue evaluation based on the critical plane evaluation. Two of them evaluate high-cycle fatigue, and the last low-cycle fatigue. You can find these in the Fatigue Module.
- The Cylindrical Test Specimen model evaluates all three stress-based criteria on a non-proportionally loaded cylindrical test specimen.
- The Structural and Fatigue Analysis of a Shaft with Fillet model demonstrates how to perform high-cycle fatigue. It also show how to calculate fatigue material data based on fatigue tests in reversed axial tension and pure torsion.
- The Low Cycle Fatigue Analysis of Cylinder with a Hole model shows how to perform fatigue study in presence of plasticity. In such a case it is important to first obtain a stable load cycle before a fatigue analysis can be performed.
If you’re interested in learning more about fatigue prediction modeling, watch the archived webinar Fatigue Modeling with COMSOL.




Comments (0)