
The COMSOL Optimization Module includes both gradient-based and gradient-free optimization techniques. Whereas the gradient-based optimization method can compute an exact analytic derivative of an objective function and any associated constraint functions, it does require these functions to be smooth and differentiable. In this blog post, we examine the use of the gradient-free optimizer, which can consider objective function and constraints that are not differentiable or smooth. The dimensions of a spinning wheel are optimized to reduce the mass while maintaining a constraint on the peak stress in the part.
Stress in a Spinning Wheel
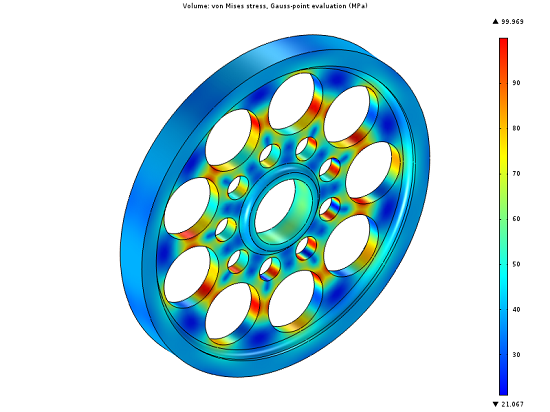
A spinning wheel will experience centrifugal stresses that result in stresses throughout the part. A regular pattern of holes has been cut into the wheel hub to reduce the mass. The von Mises stresses due to the centrifugal forces are shown. It is desirable to further reduce the mass, while keeping the stresses below a critical value.
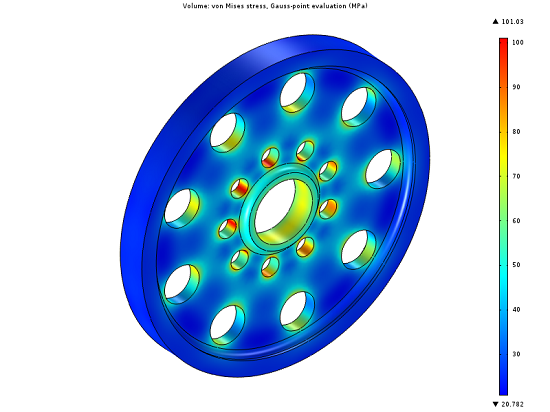
Solving for the Stresses
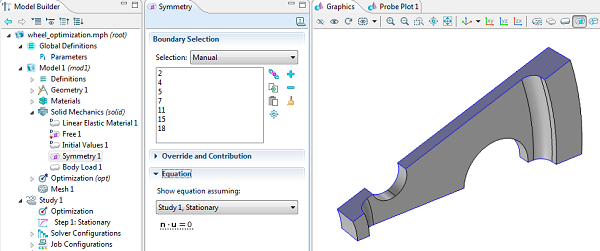
Although we could model the entire wheel at once, there is both mirror and rotational symmetry in this part making it possible to reduce the model and thereby minimize the computational requirements. Symmetry boundary conditions are used to restrain the part.
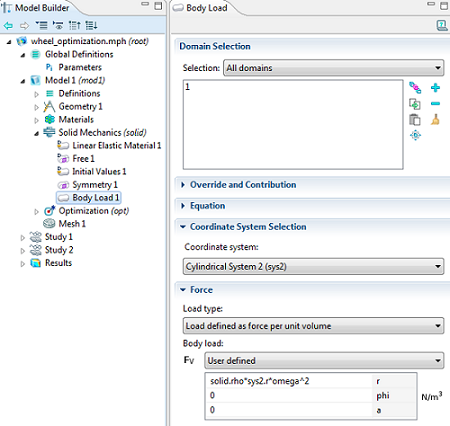
A body load is applied in terms of the rotational velocity, rotational axis, and material density to model the centrifugal force. The model is solved using the stationary solver, that is, assuming a constant rotational speed.
Choosing the Design Variables
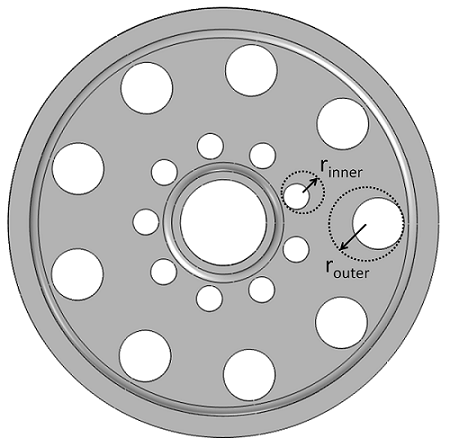
In this case, let’s assume that there is already a manufacturing process in place, and we would like to make a minimal change to the overall design of the part in order to reduce retooling costs. A natural choice of design variables would be to change the radii of the holes in the hub. Therefore, we go back to the geometry sequence and parameterize both the hole radii as well as their locations. We can also figure out, based purely on a geometric analysis, that there must be bounds on the maximum radius of each hole, otherwise the regions between the holes would get too thin and the holes would overlap. We will also put a bound on the minimum radius, since we do not want the holes to disappear completely.
Defining the Objective Function and Constraints
The optimization objective here will be simply to reduce the mass of the part, which is the integral of the material density over all domains.
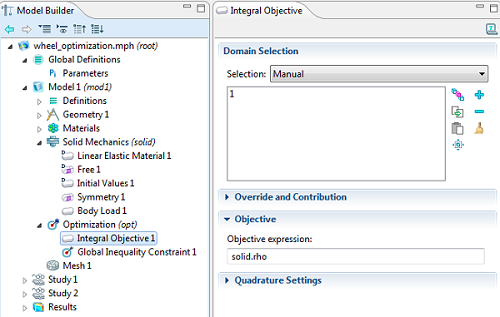
The optimization objective is to minimize the mass, the integral of the density.
The constraint is a little bit more complex; we want to minimize the peak stress in the part. However, we do not know ahead of time where the peak stress will be. If we make either the inner or outer holes too small, this will lead to a stress concentration around the hole. If we make either of the radii too large, the material between the holes can get too thin, also leading to high stresses. Therefore, we must monitor the maximum stress throughout the part, and constrain this to be below a specified peak stress. This is a non-differentiable constraint, and it specifically requires the gradient-free optimization method.
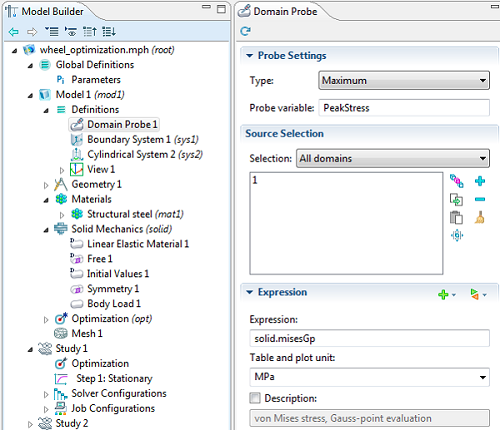
The peak stress is monitored via a Domain Probe, and given the name PeakStress.
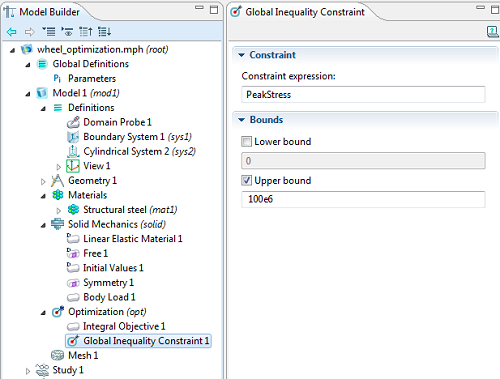
The peak stress variable is constrained to stay within an upper bound.
Solving the Problem with a Gradient-Free Optimization Method
To solve the optimization problem, an Optimization feature is added to the Study Branch. The Nelder-Mead method is one of the two gradient-free methods (the other one is Coordinate Search). The gradient-free optimization algorithms also allow the geometry to remesh as the dimensions change.
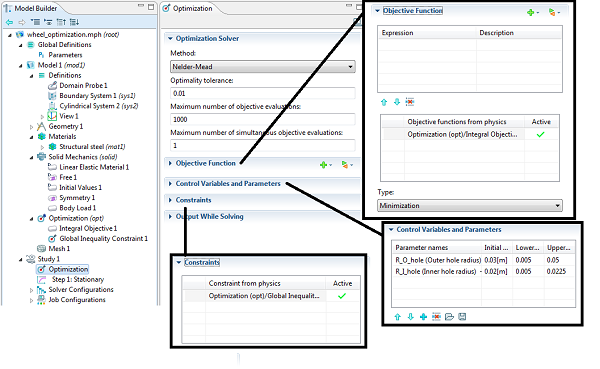
The objective function and constraint is defined from the Optimization branch in the Model Tree. The control variables are given initial conditions, and we specify upper and lower bounds. The optimal design is significantly different — the mass is reduced by 20% while maintaining a constraint on the peak stress.




Comments (2)
Edgar Kaiser
March 13, 2018Hi Walter,
is the model file available? Would be nice to play a little with it before I start my own thing.
Cheers
Edgar
Walter Frei
March 13, 2018Hello Edgar,
This is a fairly old article, and I would now recommend as a starting point for Optimization this example:
https://www.comsol.com/model/multistudy-optimization-of-a-bracket-19761