
In the Semiconductor Module, as of version 5.6 of the COMSOL Multiphysics® software, we have expanded the capability of the Schrödinger Equation physics interface from single-component to multiple-component wave functions. This allows the simulation of a wider range of systems, such as particles with spins and the valence band structure with a mixing of the 3 p-like orbitals. In this blog post, we use a simple benchmark model to illustrate how to use this multicomponent wave function functionality.
The Hamiltonian Matrix
When the wave function has more than one component, the Hamiltonian becomes a matrix to operate on the vector of the wave function components. For example, the time-dependent Schrödinger equation now reads
(1)
where N is the number of wave function components.
The minus sign on the right-hand side of the equation for the time evolution operator is due to the fact that all physics interfaces in COMSOL Multiphysics take the engineering sign convention of exp(-i k x + i \omega t) instead of the physics sign convention of exp(i k x – i \omega t). Later on, we will see that the sign of the momentum operator also differs from the one seen in most textbooks because of this.
In general, each element of the Hamiltonian matrix \mathbf{H}_{mn} can include several terms of zero, one, or two partial derivatives:
(2)
\frac{+\hbar^2}{2\,m_e} \sum_{ i,j\in \{1,2,3\}} \left[
\frac{i\, \partial}{\partial r_i} \,A_{ij}^{mn}(\mathbf{r}) \, \frac{i\, \partial}{\partial r_j}
+ \frac{i\, \partial}{\partial r_i} \,H_i^{mn(1R)}(\mathbf{r})
+ H_j^{mn(1L)}(\mathbf{r}) \, \frac{i\, \partial}{\partial r_j}
+ H^{mn(0)}(\mathbf{r})
\right]
where m_e is the electron mass; \mathbf{r} is the position vector \mathbf{r}=\{r_1,r_2,r_3\}\equiv\{x,y,z\}; and A, H^{(1R)}, H^{(1L)}, and H^{(0)} are coefficients that may be spatially varying.
In the first term, the differential operator on the left is understood to act on both the coefficient A and the wave function component \psi_{n}. Similarly, the differential operator in the second term acts on both H^{(1R)} and \psi_{n}. Note that all of the momentum operators differ by a minus sign from the usual convention, as discussed earlier.
The number of elements of the Hamiltonian matrix grows as the square of the number of wave function components. Each element may contain terms of various orders of partial derivatives, as shown in Eq. 2. To provide flexible and efficient ways to enter these terms into the graphical user interface within the limited window size, we have created a number of built-in features as of version 5.6. In the example model below, we show how to use these features.
The Model System
As mentioned above, all of the coefficients in the Hamiltonian matrix elements can be spatially varying. This is particularly true in heterostructures and nanostructures, such as quantum wires and quantum dots. For simplicity, we have chosen a model of a uniformly strained bulk crystal, where all coefficients are spatially uniform. Nevertheless, this simple model still serves the purpose of illustrating the procedure to enter the Hamiltonian matrix elements into the user interface. In addition, it also serves as a benchmark model to verify the numerical solution with the analytic solution of this simple system.
Gallium nitride (GaN) is an important wide band gap semiconductor material for optoelectronics, high-power, and high-frequency applications. Chuang and Chang published their derivation and computation of the 6-by-6 Hamiltonian matrix for wurtzite crystals including GaN in 1996 (Ref. 1). In Eq. 45 of the paper, the 6-by-6 Hamiltonian matrix is block diagonalized, and the upper left 3-by-3 matrix reads
(3)
F & K_t & -i H_t \\
K_t & G & \Delta-i H_t \\
i H_t & \Delta+i H_t & \lambda
\end{array}\right]
The matrix elements are given by Eqs. (34) and (42) in Ref. 1. For example, the element at the (1,1) position of the 3-by-3 Hamiltonian matrix is
(4)
The first two terms are numbers and the other two contain operators and numbers:
(5)
(6)
To compare with the result shown in Fig. 5 in the paper, we will set the y-component of the crystal momentum k_y to zero. For the Schrödinger Equation interface, the other two components, k_x and k_z, are replaced by the partial derivatives i\partial / \partial x and i\partial / \partial z, respectively (see footnote). So, the two equations above become
(7)
i\frac{\partial}{\partial z} A_1 i\frac{\partial}{\partial z}
+ i\frac{\partial}{\partial x} A_2 i\frac{\partial}{\partial x}
\right]+\lambda_\epsilon
(8)
i\frac{\partial}{\partial z} A_3 i\frac{\partial}{\partial z}
+ i\frac{\partial}{\partial x} A_4 i\frac{\partial}{\partial x}
\right]+\theta_\epsilon
Finally, the numbers contributed from the strain are
(9)
(10)
where \epsilon is the strain components.
The energy parameters \Delta_1 and \Delta_2, the effective mass parameters A_1~A_1, and the deformation potentials D_1~D_1 are listed in Table III of Ref. 1.
Expanding out Eq. 4 for the element F at the (1,1) position of the 3-by-3 Hamiltonian matrix, using Eq. 7 and 8, we get
(11)
\frac{\hbar^2}{2m_e}\left[
i\frac{\partial}{\partial z} (A_1+A_3) i\frac{\partial}{\partial z}
+ i\frac{\partial}{\partial x} (A_2+A_4) i\frac{\partial}{\partial x}
\right]
+\Delta_1+\Delta_2
+\lambda_\epsilon
+\theta_\epsilon
We have collected the operators in the first term, and the other four terms are numbers.
Numerical and Analytic Methods
In Fig. 5 of Ref. 1, the valence band dispersions along the k_x and k_z directions are plotted for unstrained and strained crystals, with k_y set to zero. Since the systems under consideration are bulk crystals, k_x and k_z are just numbers, and the Hamiltonian (3) reduces to a 3×3 matrix of certain numerical values corresponding to the given values of k_x and k_z. The eigenvalues of this matrix can be computed numerically to obtain the band structure shown in the figure. This is the analytic approach taken by the paper and will be used to verify the numerical approach to be discussed next.
In a general nonuniform structure, such as quantum wells and quantum dots, the numbers k_x and k_z have to be replaced by the partial derivatives i\partial / \partial x and i\partial / \partial z, as mentioned earlier, and the Schrödinger equation on the xz-plane is solved to obtain the band structure. This is the numerical approach. Of course, this becomes overkill for the simple system of a bulk crystal. However, for the purpose of teaching and verification, we have chosen this simple system. Once you have learned how to use the physics features to build this simple model, you are equipped to simulate more complex systems solvable only by the numerical approach.
The COMSOL Multiphysics® Model
It is straightforward to set the number of wave function components to 3 in either the Model Wizard or the physics interface Settings window, since the size of the Hamiltonian is 3×3.
The model is 2D in the x– and z directions, as discussed above. To make the model notation easier to read, we change the coordinate name for the second axis from the default y to z, as shown in the screenshot below.
Change the coordinate names to match the directions of interest (x and z).
Since we are only interested in the band structure near the zone center, we can use a simple square domain slightly smaller than the unit cell, and use the Floquet–Bloch periodic boundary conditions for the Schrödinger equation. In this regime, the problem approaches a uniform continuum and a small number of mesh elements is sufficient. (See the tutorial model of a thin-film BAW structure for a mechanical model using the same technique.)
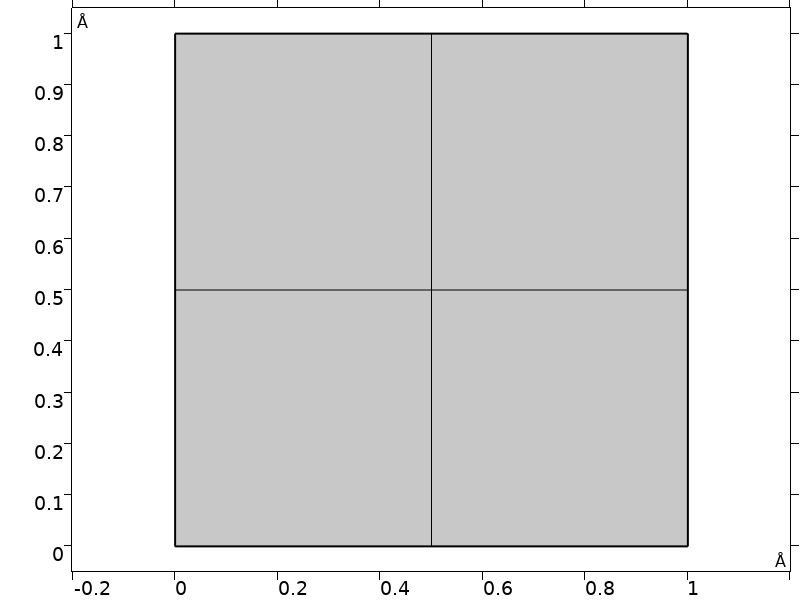
Domain and mesh used in the model.
To conveniently create a plot to compare with Fig. 5 in the paper, we set up a swept parameter kp, such that its positive axis represents the kx-axis and the negative axis represents the kz-axis. Use the if statement in the expressions for the parameters kx and kz to achieve this, as shown in the screenshot below.
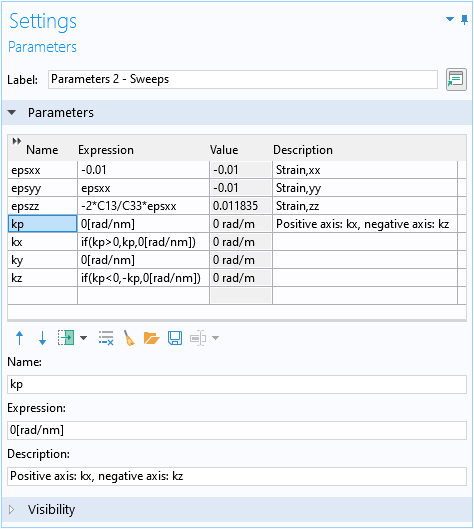
Set up a parameter kp for the dual axis 1D plot for kx and kz.
Analytic Solution
For the analytic approach, we set up a global equation to diagonalize the 3×3 Hermitian matrix given by Eq. 3. We use the reserved name lambda for the eigenvalue in the global equation. We scale the Hamiltonian with the energy scale of 1 meV so that the source term is about the order of unity, and the eigenenergy is the eigenvalue in the unit of meV. We also add some blank spaces in the expressions to align the columns of the matrix.
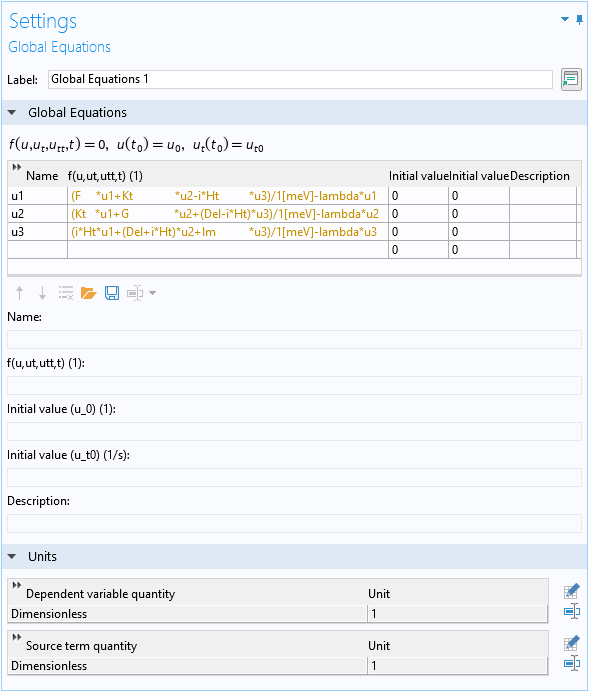
Global equation to find the eigenvalues of the 3×3 matrix.
The text is yellow because at this point, the eigenvalue variable lambda is not yet defined.
Solving the Schrödinger Equation
As mentioned earlier, the numerical approach solves the Schrödinger equation. To conveniently create a plot to compare with Fig. 5 in the paper, we set the Eigenvalue scale to the same energy unit as the vertical axis of the figure (meV), so that the eigenvalue takes on the numerical value of the eigenenergy in the same unit (meV).
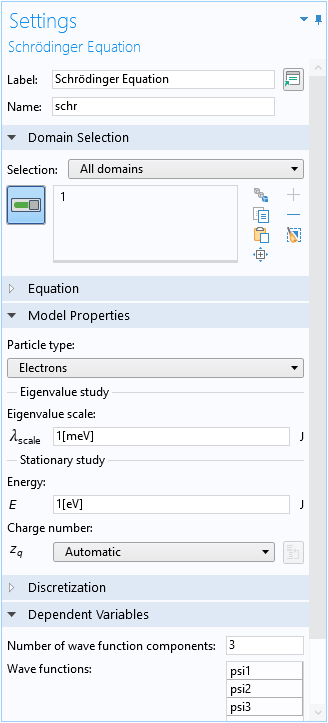
Settings window of the Schrödinger Equation physics interface.
Hamiltonian Matrix Input
Now, we are ready to enter the matrix elements of the 3×3 Hamiltonian. Again, we use the element F at the (1,1) position as an example. The contributions to this element are summarized in Eq. 11. The first term contains second-order derivatives, so we add a Second Order Hamiltonian domain condition. This feature was introduced as of COMSOL Multiphysics 5.6, together with the capability of handling multiple-component wave functions for the Schrödinger Equation physics interface.
The central feature in the Settings window for this domain condition is the Hamiltonian input table. The first two columns of this table are for the row and column indices of the Hamiltonian matrix element to be entered. Each index is selected from a drop-down menu, which is automatically populated from 1 to N (the number of wave function components). For example, here we have set N to 3, so the drop-down menu has the choices of 1, 2, or 3. Always decide on and set the number of wave function components before you start entering data into the table (see the section Known Limitation below).
The third and fifth columns are for the two differential operators. They are also provided as drop-down menus with automatic population of differential operators according to the spatial dimension of the model. Here, we have set up a 2D model on the xz-plane, so the choices are i\partial / \partial x and i\partial / \partial z.
The fourth column is for the effective mass parameter A. As with almost all other input fields in COMSOL Multiphysics, the input field accepts a number, parameter, variable, or any other mathematical formula. A prefactor of \hbar^2/2m_e is always built in for this type of domain condition, including the current one, First Order Hamiltonian, Left, First Order Hamiltonian, Right, and Zeroth Order Hamiltonian.
The last column, Description, gives us an opportunity to document each entry in the input table. Each element in the Hamiltonian matrix, for example, the element F given by Eq. 11, contains different types of terms, which will be entered into multiple table rows across several different features. As such, it is important to keep track of each table row by entering appropriate comments in the Description column.
The screenshot below shows the Settings window of the domain condition, with the first term in Eq. 11 entered into the first two rows of the Hamiltonian input table. The position of the matrix element F is (1,1), so both the row and column indices are 1. The differential operators and the A parameters of the two rows in the table correspond to the two terms in the square brackets in Eq. 11. The Description column records the source of the contribution; in this case, the two rows come from the F=\lambda+\theta part of Eq. 4 originally.
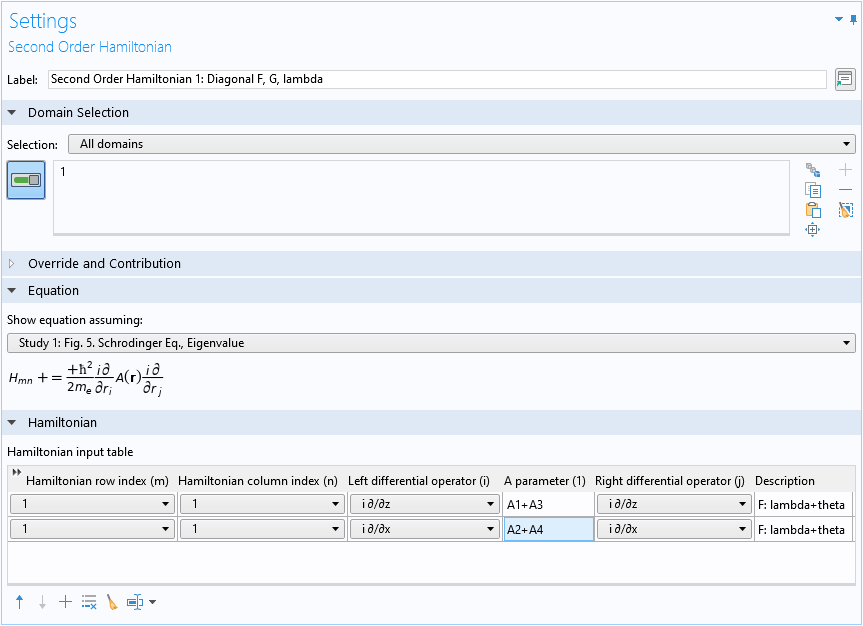
The settings window for the Second Order Hamiltonian domain condition, with the first term of the matrix element F entered.
Copy/Paste Table Rows
Before entering the rest of the terms for the (1,1) element F, we notice that the second-order operator part of the (2,2) element G is identical to the one of F. From Eq. 34 of Ref. 1:
(12)
so we get the same contributions to the second-order Hamiltonian (G=\lambda+\theta), except the position is different: instead of (1,1), now it’s (2,2).
Instead of filling in two more rows of data for G from scratch, we can copy and paste the two rows for F and just change the row and column indices to 2. First, click and drag the mouse to select the two rows in the table:
Then right-click to copy the selected rows:
Then click the Add button to add a new row:
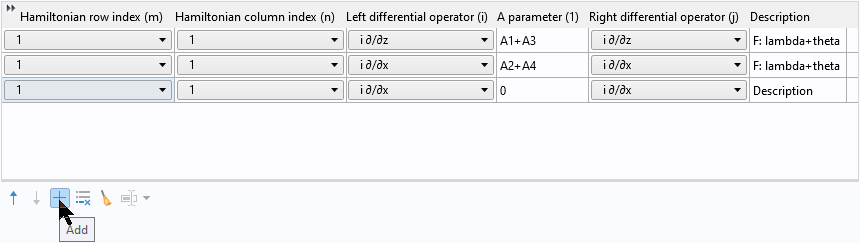
Then right-click to paste the two copied rows into the table:
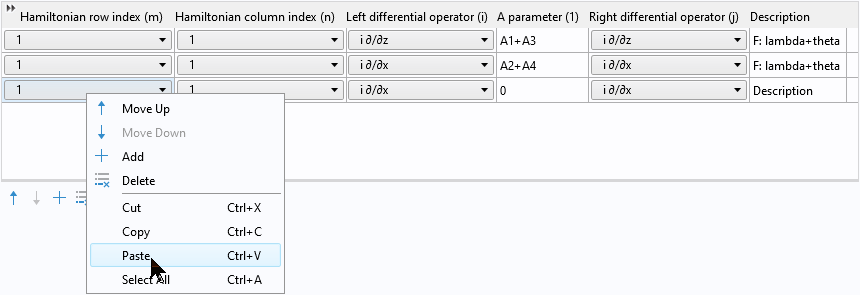
After pasting, we have two pairs of identical rows:
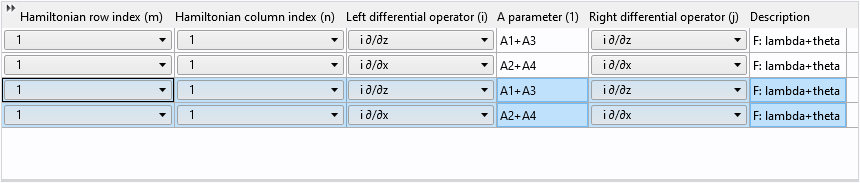
Finally, change the row and column indices from 1 to 2 and update the description:
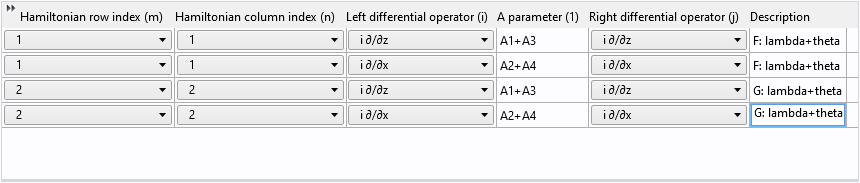
Reusing table rows in this way not only saves time but also helps avoid mistakes!
Disable Default Effective Mass Contribution
The Second Order Hamiltonian domain condition that we just demonstrated for the diagonal elements corresponds to the kinetic energy terms normally added by the default Effective Mass feature. We should disable it to remove the unwanted default contribution to the Hamiltonian.
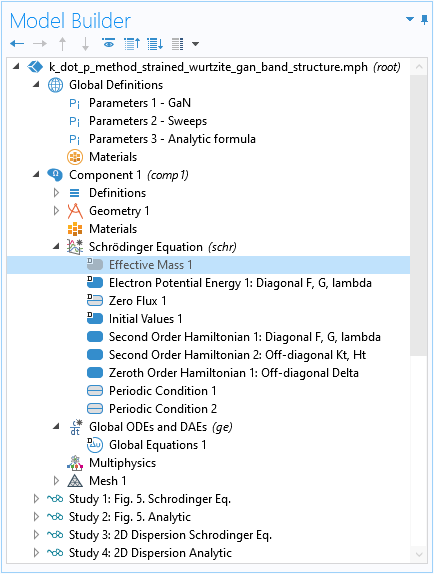
Disable the default Effective Mass feature to remove its unwanted contribution to the Hamiltonian.
Terms Without Operators
To enter the rest of the terms for the (1,1) element F (last 4 terms in Eq. 11: \Delta_1+\Delta_2+\lambda_\epsilon+\theta_\epsilon), which are just numbers, we can use either the Zeroth Order Hamiltonian domain condition, or the default Electron Potential Energy domain condition, as shown in the screenshot below, since the element is on the diagonal of the Hamiltonian matrix.
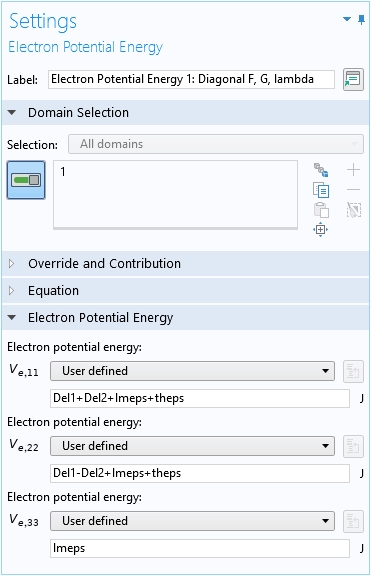
Use the default Electron Potential Energy domain condition for the zeroth-order terms of the diagonal elements of the Hamiltonian matrix.
Off-Diagonal Elements
For the off-diagonal elements, we follow the same procedure to fill in the Hamiltonian input table for the second-order terms:

And the zeroth-order terms:

As mentioned earlier, the Zeroth Order Hamiltonian has the prefactor of \hbar^2/2m_e built in; therefore, if the input quantity (Del in this case) is an energy unit, it needs to be divided by the prefactor.
Known Limitation
If the number of wave function components is changed after a Hamiltonian matrix input table has been filled with data, the table rows will become out of sync. At this point, the table needs to be cleared and filled with data again. We recommend that you first determine the particular Hamiltonian matrix that you would like to study in a model and enter the number of wave function components accordingly, before filling any Hamiltonian input table with data.
Other Settings
It is straightforward to set up the Floquet–Bloch periodic boundary conditions to create the simple mapped mesh and configure sweeps of the wave vectors using the specially prepared parameter kp in the eigenvalue studies.
To solve the analytic 3×3 matrix equation configured with the global equation, use the All eigenvalue option to obtain all 3 eigenvalues of the 3×3 matrix equation.
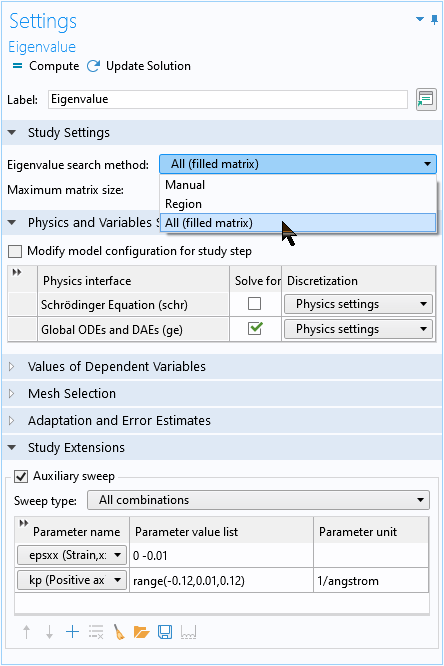
Use the All eigenvalue option to obtain all 3 eigenvalues of the global equation.
Computed Band Structure for Unstrained and Strained Wurtzite Crystals
The two figures below show the computed unstrained and strained heavy hole (HH), light hole (LH), and crystal-field split-off hole (CH) dispersions along the positive kx-axis and negative kz-axis directions, agreeing well with analytic solution (circles) and Fig. 5 in Ref. 1.
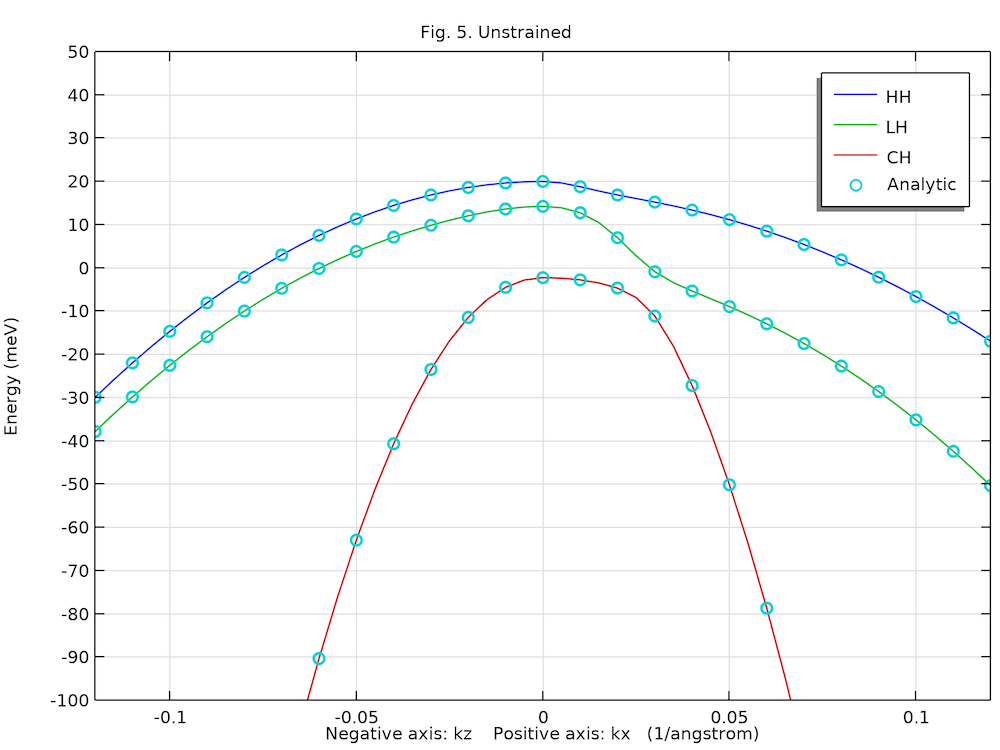
Unstrained valence band structure of the bulk GaN wurtzite crystal.
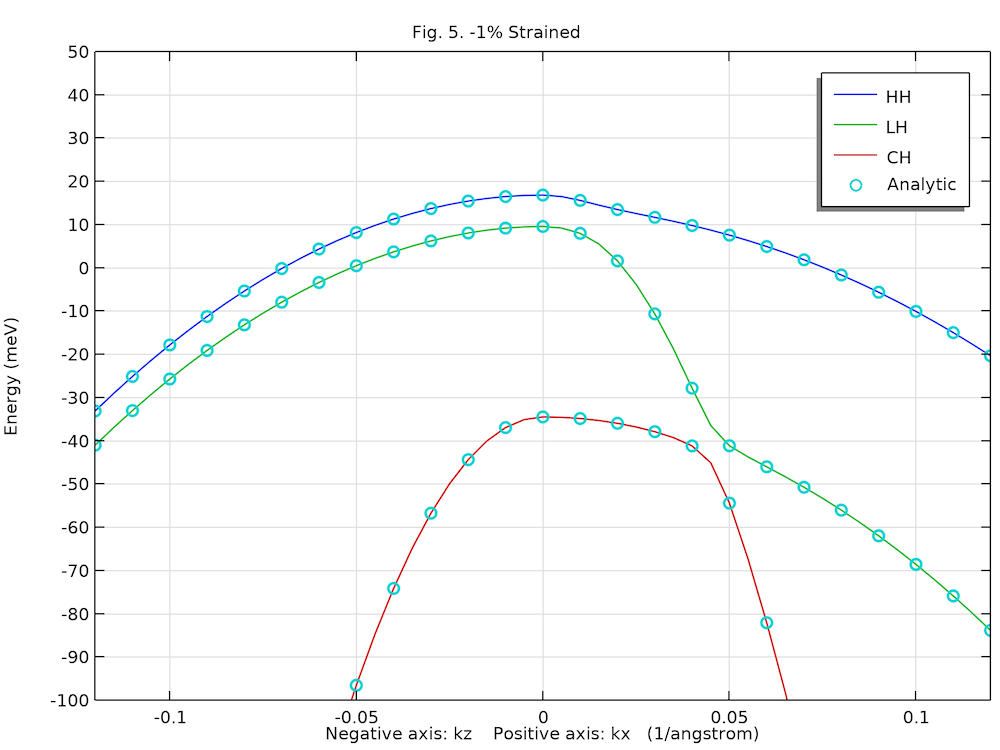
Compressively strained valence band structure of the bulk GaN wurtzite crystal.
The plot below compares the 2D energy surfaces along the x– and z directions for the 3 valence bands between computed values (color surface) and the analytic solution (gray wireframe). The agreement is also very good.
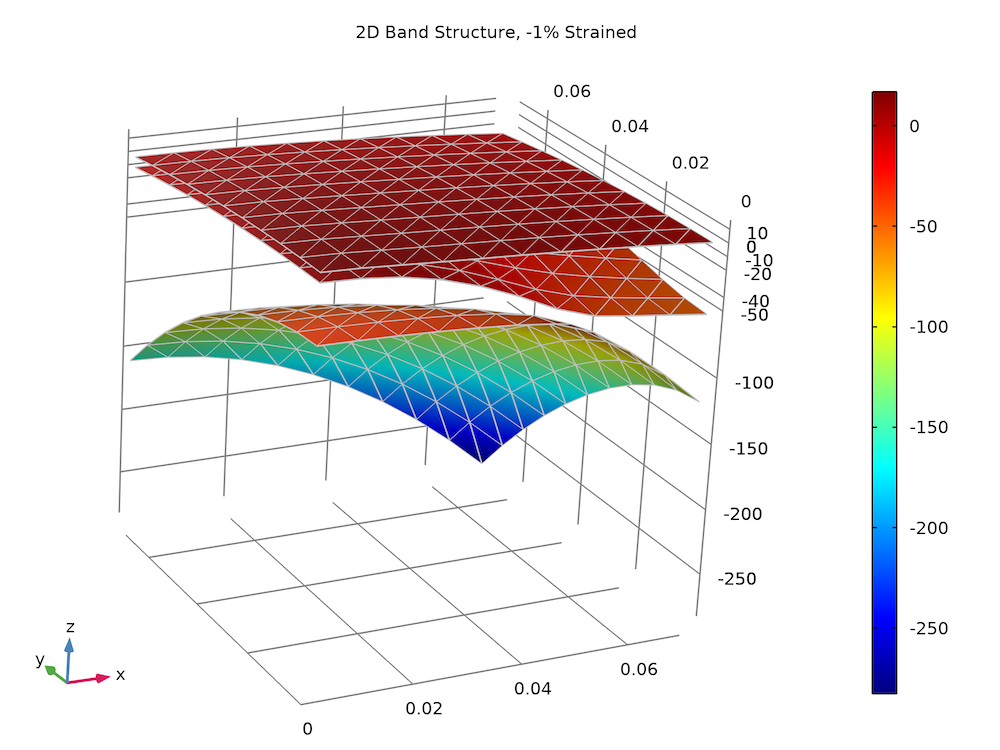
Strained valence band structure of the bulk GaN wurtzite crystal.
Conclusion
In this blog post, we demonstrated the new capability of the Schrödinger Equation physics interface to handle multicomponent wave functions, using a simple bulk crystal example. The Hamiltonian matrix is systematically entered into the user interface with built-in features. The same methodology can be applied to more complex systems, such as quantum wells and quantum dots. We would love to hear about how you use this new capability for your simulation projects!
Try It Yourself
Try modeling a strained wurtzite GaN band structure yourself by clicking the button below, which will take you to the Application Gallery and a downloadable MPH-file:
Reference
- S.L. Chuang and C.S. Chang, “k·p method for strained wurtzite semiconductors,” Phys. Rev. B, vol. 54, p. 2491, 1996.
Footnote
Recall that COMSOL’s sign convention for the time harmonic phasor is exp(+i \omega t), so a plane wave is exp(+i \omega t-i k_x x). Thus the operator +i\partial / \partial x, not -i\partial / \partial x, is used.




Comments (7)
Nikhil Sen
November 11, 2021Hi Chien
Thanks for excellent blogpost. It helped me a lot to learn the COMSOL, specifically Schrodinger equation solver.
I was wondering how does the eigenvalue problem is solved with kp as the sweeping parameter? I am asking this question because I see no explicit mention of kx or ky terms in the Hamiltonian matrix.
Chien Liu
November 11, 2021 COMSOL EmployeeThank you Nikhil for the comment! You are right that kx and kz does not appear explicitly in the Hamiltonian but they are used in the Floquet–Bloch periodic boundary condition. Hope this helps. Sincerely, Chien
Nikhil Sen
November 11, 2021Thanks Chien for prompt reply. And it does answer my previous question.
I have an additional question, when I use kp as one of the k-vector for the Floquet-Bloch periodicity, I get separate data points (eigne values) in the graph as opposed to continuous line. Additionally, I also get legend for every value of kp (& corresponding eigen energy) in the graph rather than for the entire band (e.g. HH, LH etc). Why does this happen?
Is it something to do with how kx and kz are defined that we don’t get legend for every eigen value when k-vector for the Floquet-Bloch periodicity are kx and ky?
Thanks again for your help.
Nikhil Sen
November 11, 2021I did a little deeper digging and I found that kx and kz are defined when the Floquet-Bloch periodic condition is applied.
Does it mean that what is kx and kz is defined when the Floquet Bloch condition is defined (at least in this specific example?
Chien Liu
November 11, 2021 COMSOL EmployeeLooks like our messages crossed but yes as I said above kx and kz are used in the Floquet–Bloch periodic boundary condition. Hope this helps. Sincerely, Chien
Nikhil Sen
November 11, 2021Hi Chein
Sorry for confusion. I think there is a slight confusion.
My previous question was answered but my new question is this:
I have an additional question, when I use kp as one of the k-vector for the Floquet-Bloch periodicity, I get separate data points (eigne values) in the graph as opposed to continuous line. Additionally, I also get legend for every value of kp (& corresponding eigen energy) in the graph rather than for the entire band (e.g. HH, LH etc). Why does this happen?
Is it something to do with how kx and kz are defined (in parameter-sweep) that we don’t get legend for every eigen value when k-vector for the Floquet-Bloch periodicity are kx and ky?
Thanks again for your help.
Chien Liu
November 11, 2021 COMSOL EmployeeHi Nikhil, If you follow the step-by-step instructions in the PDF documentation accompanying the example model, you should be able to generate the same plots. If you need further assistance, please do not hesitate to contact us at support@comsol.com. Sincerely, Chien