Studies & Solvers Blog Posts
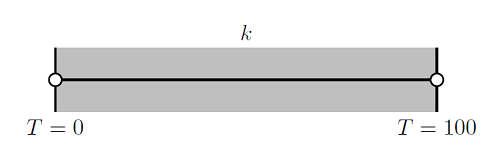
Meshing Considerations for Nonlinear Static Finite Element Problems
As part of our solver blog series we have discussed solving nonlinear static finite element problems, load ramping for improving convergence of nonlinear problems, and nonlinearity ramping for improving convergence of nonlinear problems. We have also introduced meshing considerations for linear static problems, as well as how to identify singularities and what to do about them when meshing. Building on these topics, we will now address how to prepare your mesh for efficiently solving nonlinear finite element problems.
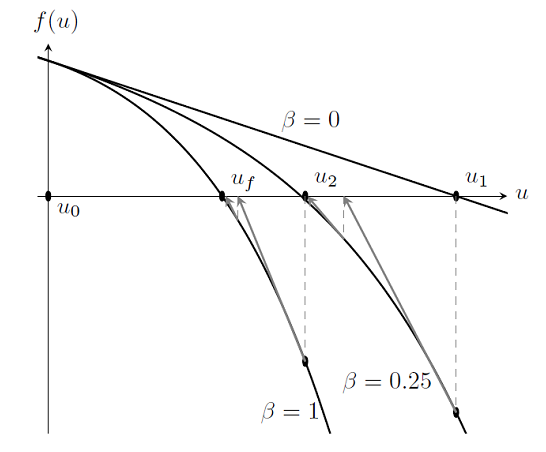
Nonlinearity Ramping for Improving Convergence of Nonlinear Problems
As we saw in “Load Ramping of Nonlinear Problems“, we can use the continuation method to ramp the loads on a problem up from an unloaded case where we know the solution. This algorithm was also useful for understanding what happens near a failure load. However, load ramping will not work in all cases, or may be inefficient. In this posting, we introduce the idea of ramping the nonlinearities in the problem to improve convergence.
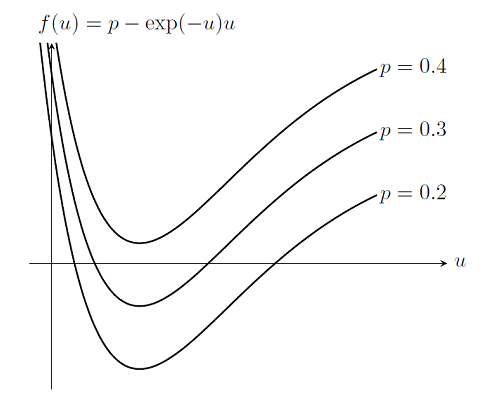
Load Ramping of Nonlinear Problems
As we saw previously in the blog entry on Solving Nonlinear Static Finite Element Problems, not all nonlinear problems will be solvable via the damped Newton-Raphson method. In particular, choosing an improper initial condition or setting up a problem without a solution will simply cause the nonlinear solver to continue iterating without converging. Here we introduce a more robust approach to solving nonlinear problems.
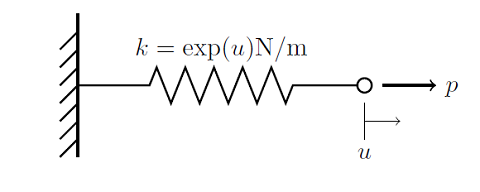
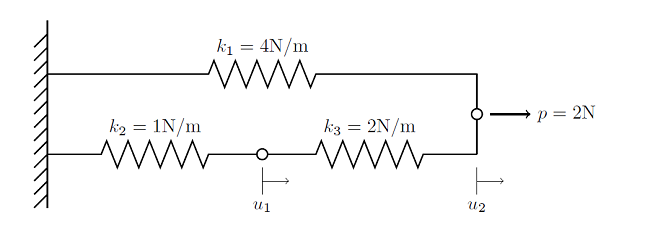
Solving Nonlinear Static Finite Element Problems
Here, we begin an overview of the algorithms used for solving nonlinear static finite element problems. This information is presented in the context of a very simple 1D finite element problem, and builds upon our previous entry on Solving Linear Static Finite Element Models.
Solutions to Linear Systems of Equations: Direct and Iterative Solvers
In this blog post we introduce the two classes of algorithms that are used in COMSOL to solve systems of linear equations that arise when solving any finite element problem. This information is relevant both for understanding the inner workings of the solver and for understanding how memory requirements grow with problem size.
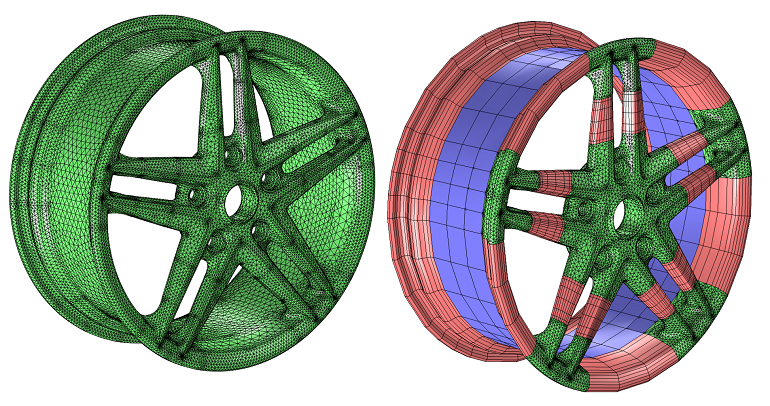
Meshing Your Geometry: When to Use the Various Element Types
In a previous blog entry, we introduced meshing considerations for linear static problems. One of the key concepts there was the idea of mesh convergence — as you refine the mesh, the solution will become more accurate. In this post, we will delve deeper into how to choose an appropriate mesh to start your mesh convergence studies for linear static finite element problems.
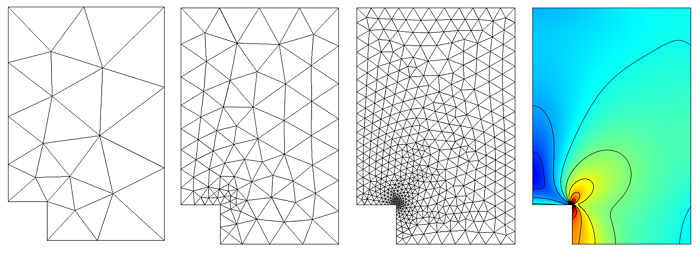
How to Identify and Resolve Singularities in the Model when Meshing
In our previous post on Meshing Considerations for Linear Static Problems, we found that, in the limit of mesh refinement, the solution to the finite element model would converge toward the true solution. We also saw that adaptive mesh refinement could be used to generate a mesh that would have smaller elements in regions where the error was higher, rather than simply using smaller elements everywhere in the model. In this post, we will examine a couple of common pitfalls […]
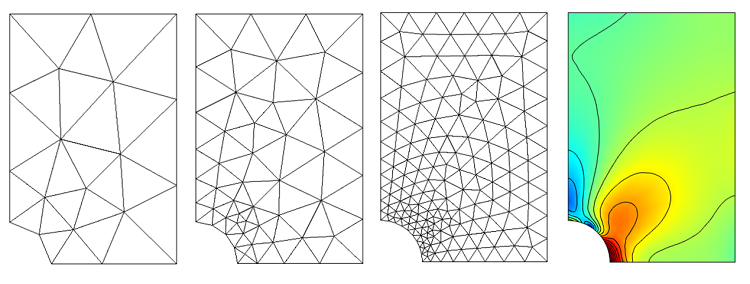
Meshing Considerations for Linear Static Problems
In this blog entry, we introduce meshing considerations for linear static finite element problems. This is the first in a series of postings on meshing techniques that is meant to provide guidance on how to approach the meshing of your finite element model with confidence.

Solving Linear Static Finite Element Models
In this first blog entry of our new solver series, we describe the algorithm used to solve all linear static finite element problems. This information is presented in the context of a very simple 1D finite element problem, but is applicable for all cases, and is important for understanding more complex nonlinear and multiphysics solution techniques to be discussed in upcoming blog posts.

On Solvers: Benefits and Limits of Solution Methods
This week we have the honor of having Professor Wolfgang Joppich as a guest blogger. As you may know, COMSOL Multiphysics provides great default solvers for all applications. For the interested user, it is good to know that you can optionally tune or completely change the solver settings. We strongly recommend that you read this blog posting to get an experts’ perspective on the solver technologies offered by COMSOL. I am an avid reader of the COMSOL Blog and an […]

Probing Your Simulation Results
For a transient simulation, imagine if you could simply insert a virtual sensor in a model at a certain location and then monitor the evolution of a field value over time while solving. In COMSOL Multiphysics® you can do just that by using Probes. You define a probe in the Model Builder tree right under the Model Definitions node. Measuring the value at a point is not the only thing you can do with probes, but in this blog post we […]
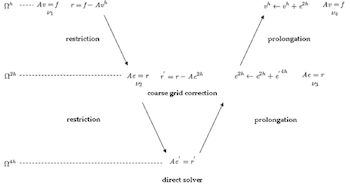
On Solvers: The V-Cycle Multigrid
As discussed previously on the blog, iterative methods efficiently eliminate oscillatory error components while leaving the smooth ones almost untouched (smoothing property). Multigrid methods, in particular, use the smoothing property, nested iteration, and residual correction to optimize convergence. Before putting all of the pieces of this proverbial puzzle together, we need to introduce residual correction and dive a bit deeper into nested iteration. Let’s begin with the latter of these elements.
On Solvers: Multigrid Methods
Solution methods are a valuable tool for ensuring the efficiency of a design as well as reducing the overall number of prototypes that are needed. In today’s blog post, we introduce you to a particular type of method known as multigrid methods and explore the ideas behind their use in COMSOL Multiphysics.
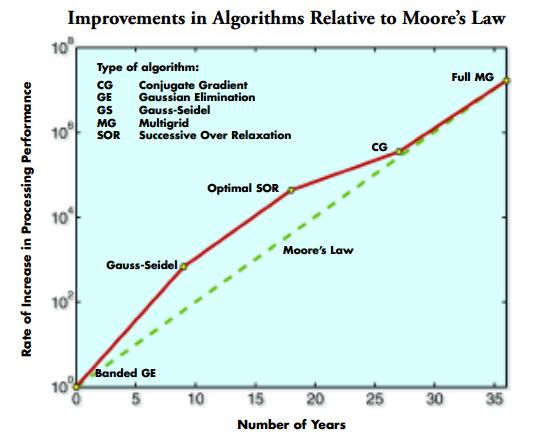
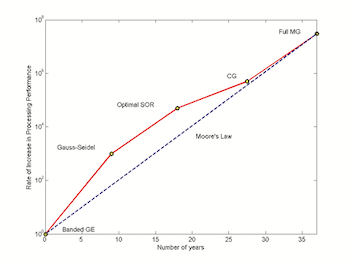
Moore’s Law for Solvers
At the heart of any simulation software are the solvers. Those are things that take geometry/mesh/physics to the computational results. While it’s convenient to think about solvers in terms of the type of study (think time-dependent, parametric, or eigenvalue), there is a hierarchy of solvers that are usually employed. And at the foundational level of any simulation — and for every iteration — there is a linear solver.
