How to Estimate the Number of Degrees of Freedom in a Model
In the COMSOL Multiphysics® software, the number of degrees of freedom (DOFs) in a model have a significant correlation to, and effect on, the computation of a model. In this article, we explain the importance of the degrees of freedom for a model and how to estimate the number of degrees of freedom.
What Does Degrees of Freedom Mean in COMSOL Multiphysics®?
The solution time and memory requirements to compute a model are strongly related to the number of degrees of freedom in the model. It is often desirable to be able to estimate the number of degrees of freedom based on the number of elements in the model.
For most physics interfaces, each dependent variable is present in all nodes in the mesh. This means that the number of degrees of freedom is given by the number of nodes multiplied by the number of dependent variables. The relation between the number of nodes and the number of elements depends on the order of the elements and differs between 2D and 3D. The relation is only approximate, since it depends on the ratio of the elements that lie on the boundary of the geometry. For thin geometries, where a large proportion of the elements lie on the boundary, the number of nodes per element is a bit higher. Additional background information on the degrees of freedom in a model can be found in the blog post that discusses how much memory is needed to solve large models, under the section of text explaining what degrees of freedom are.
Estimating the Number of DOFs
The following are approximate relations between the number of nodes and the number of elements in 2D and 3D for Lagrange elements of different order. Quadrilateral (quad) meshes have roughly twice as many nodes as triangular meshes, and hexahedral (brick) meshes have about six times as many nodes as tetrahedral meshes. Upon calculating the total number of nodes, you can then calculate the total number of degrees of freedom.
| Spatial Dimension | Element Order | Approximation for the Number of Nodes |
|---|---|---|
| 2D | Linear triangular elements | (# nodes) = 0.5 * (# elements) |
| 2D | Linear quad elements | (# nodes) = 1 * (# elements) |
| 2D | Quadratic triangular elements | (# nodes) = 2 * (# elements) |
| 2D | Quadratic quad elements | (# nodes) = 4 * (# elements) |
| 2D | Cubic triangular elements | (# nodes) = 4.5 * (# elements) |
| 2D | Cubic quad elements | (# nodes) = 9 * (# elements) |
| 3D | Linear tetrahedral elements | (# nodes) = 0.2 * (# elements) |
| 3D | Linear brick elements | (# nodes) = 1.2 * (# elements) |
| 3D | Quadratic tetrahedral elements | (# nodes) = 1.4 * (# elements) |
| 3D | Quadratic brick elements | (# nodes) = 8.5 * (# elements) |
| 3D | Cubic tetrahedral elements | (#nodes) = 4.6 * (# elements) |
| 3D | Cubic brick elements | (#nodes) = 28 * (# elements) |
The total number of degrees of freedom is given by: (# degrees of freedom) = (# nodes) * (# dependent variables).
The number of mesh elements in your model is presented in the Log window each time you create a new mesh or modify an existing one by clicking the Build All button. It is also available through the Mesh ribbon tab, in the Evaluate ribbon group, through the Statistics button.
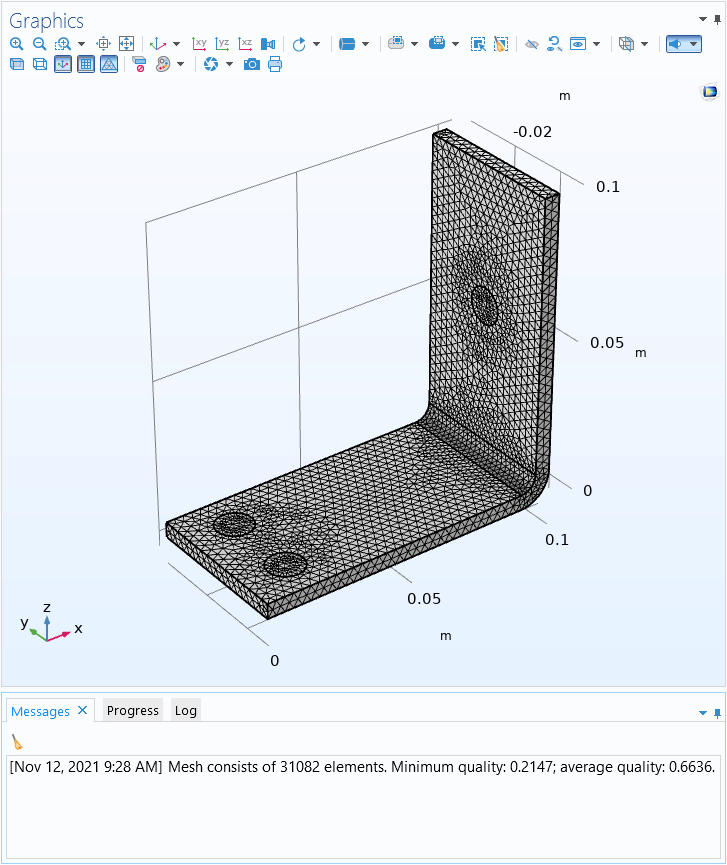
The Statistics button in the Mesh ribbon tab (top, right) is used to quickly evaluate the number of mesh elements, among other mesh statistics, in the model. The respective quantities are displayed in the Log window.
You can also find the number of mesh elements in your model by right-clicking the Mesh node and choosing Statistics.
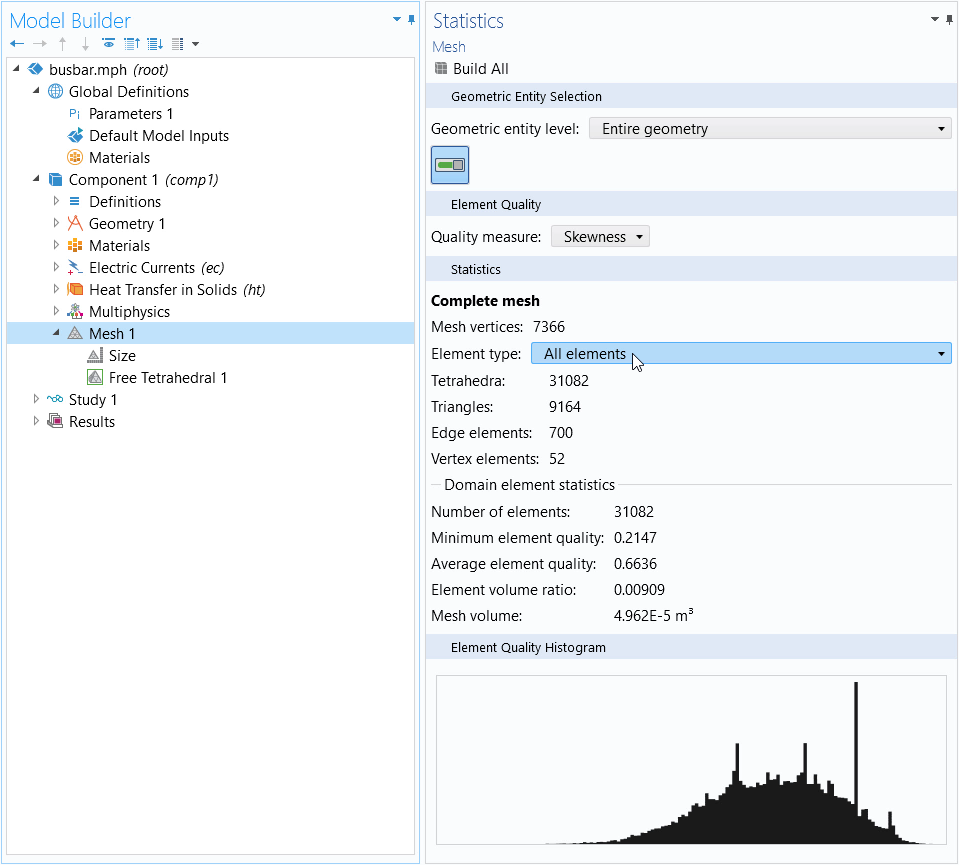
The Mesh Statistics window, which provides a detailed snapshot of statistical information regarding the mesh in your model. Above, you can see a breakdown for the number of mesh elements according to type.
Computing the Number of DOFs
To see the number of degrees of freedom in a model, you need to first create solver configurations by either solving the model or right-clicking Study and choosing Show Default Solver. Your study will then contain one Compile Equations node for each study step. Right-click on any such node and select Statistics to see the number of degrees of freedom solved for by the corresponding study step.
The Statistics page, which provides you with statistics about the solver, dependent variables, and the number of degrees of freedom.
This will provide you with an overview of the dependent variables and their number of degrees of freedom as well as the total number of degrees of freedom. Note that the number of degrees of freedom is not the only factor determining the memory requirements and the solution time for a problem. Additionally, computing the statistic above requires a computation of the size of the assembled finite element model, which can take some time for large models. For those cases, depending on the size of your model, it can be more feasible to estimate the number of degrees of freedom using the approximations provided toward the beginning of this article.
Submit feedback about this page or contact support here.
