
Mufflers are often located in exhaust systems or on heat, ventilation, and air conditioning (HVAC) systems, where their key functionality is to dampen the noise that is emitted from the system. A correct description of the acoustic damping (absorption and attenuation) processes in the muffler is important when designing and modeling these systems.
Modeling the Damping Effect
Damping is generally achieved by a combination of three processes: resonances that trap the acoustic energy at given frequencies, absorption of acoustic energy by different porous and fibrous lining materials, and losses in perforated plates, also known as perforates. COMSOL Multiphysics offers a multitude of techniques to model both the damping in porous materials and the acoustic properties of perforates.
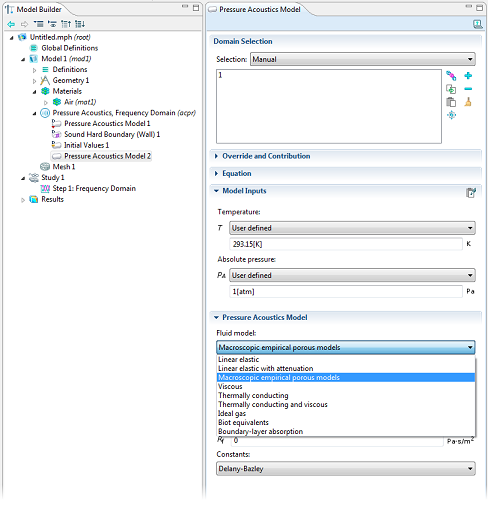
Adding an equivalent fluid model for a porous domain is easy in COMSOL Multiphysics. Simply add a new pressure acoustics model and activate it in the domain with the porous material, then select the fluid model. The “Macroscopic empirical porous models” comprise the Delany-Bazley and the Miki models, while the “Biot equivalents” model is the Johnson-Champoux-Allard (JCA) model in a rigid or limp porous matrix frame configuration.
As with many modeling approaches, several degrees of detail are possible in this type of analysis. You may model the system in great detail, for example, modeling every hole in a perforated plate. This approach may yield detailed results, but it is often impossible in practice due to the computational cost. You can also choose a form of model reduction, meaning you can determine which approximation can be used to simplify the model. For example, this could come in the form of lumping (describing part of your model using characteristics like stiffness, damping, and mass), employing sub-models (using the results from a detailed analysis of a small section of your model as an input into the larger model), or homogenization (consider a heterogeneous domain as a homogeneous domain with certain compensating properties). The typical approach for a porous material, for example, is to describe the wave propagation in a homogenized way, spreading out the losses by using an equivalent fluid model. Similarly, perforated plates are most often modeled using a homogenized transfer impedance approach, where the losses due to the presence of the holes are spread out over the boundary where the holes are located.
Implementing Modeling Types
To implement these types of models in COMSOL Multiphysics, you could use some of the built-in functionality, such as selecting one of the many fluid models or using a perforated plate boundary condition. You also have the flexibility to customize the model based on your needs by defining your preferred equivalent fluid model, defining your own transfer impedance model, or defining your material properties based on measured data you import into COMSOL Multiphysics.
As I mentioned in the beginning of this blog post, a good description of damping materials and perforated plates is important when designing systems containing mufflers. It is also important in application areas other than mufflers, of course. For instance, this is important when modeling wall lining and sound absorption for rooms (absorbers and diffusers), or when modeling the acoustics of a car interior, or a loudspeaker system. In both cases, one has to decide how to treat and model sound propagation through materials such as textiles, foams, and porous materials.
Porous Absorbing Materials
When simulating a system that contains a porous material, you will need to decide on which modeling approach to take, as well as how your material can be described based on that approach. The damping properties of porous and fibrous materials can be included in one of the following forms in COMSOL Multiphysics:
- A surface impedance may be added at the boundary between the air domain and the porous material so that the porous domain itself is not modeled, but only its “boundary” influence is. This impedance can be based on an analytical model or on measured data from an impedance tube measurement, for example.
- The porous domain can be modeled as a fluid with a given attenuation coefficient; this can be, and often is, frequency-dependent. In COMSOL Multiphysics you can enter the attenuation coefficient of a material directly, and this can be entered as an analytical expression or as a frequency-dependent function based on measured material property data you import into COMSOL Multiphysics.
- The porous domain can be modeled as an equivalent fluid: a homogenized model where the porous domain is treated as a “fluid” with damping properties. COMSOL Multiphysics contains many equivalent fluid models, including the well-known Delany-Bazley, Miki, and Johnson-Champoux-Allard (JCA) models.
- Finally, it is possible to use the Poroelastic Waves interface to solve a detailed model for the interaction between the elastic porous matrix and the saturating fluid based on the equations described by Biot’s theory. This interface can be used to model any porous material, and solves for both the displacement of the porous matrix and the pressure in the saturating fluid.
Your choice of an approach from the above list will depend on what data is available for the porous material and on the desired level of detail. Keep in mind that in all cases it is possible to use a sub-model approach. For example, you could create a detailed model of a piece of porous lining and extract the surface impedance, then add that impedance as a boundary condition in a model of the full system.
Perforated Plates
When perforated plates are present in a muffler system, they typically contain many holes, and it is not generally expedient to model them all in detail. Moreover, in order to get the correct viscous and thermal damping of the acoustic waves (when they pass through the holes) you would need to model the acoustics in the holes using the Thermoacoustic interface, which will increase the computational complexity of the model. The best approach, therefore, is to model a perforated plate using a transfer impedance boundary condition; this boundary condition is available in COMSOL Multiphysics and is based on certain characteristics of your perforations such as plate thickness and hole diameter. See, for example, the Acoustic Muffler with Thermoacoustic Impedance Lumping model. This model also shows how to use a sub-model approach: here a detailed thermoacoustic model of a single hole is used to determine a transfer impedance.



Comments (1)
Devid Bianco
September 26, 2023The “Acoustics and Vibrations Analysis Webinar” linked in the post is no longer available.