When looking for a cost-effective feed network, engineers can turn to the Butler matrix as a potential solution. This passive beamforming feed network is used with phased array antennas, which have applications in upcoming technologies like 5G. To efficiently analyze and design Butler matrix feed networks, we can turn to the COMSOL Multiphysics® software and the add-on RF Module.
Combining Butler Matrix Beamforming Networks and Phased Array Antennas
The next big thing in wireless communication, 5G, is on its way. Once here, the 5G network can provide faster download rates, reliable service everywhere, and more. But before this can happen, we must meet all of the requirements for 5G, such as antennas with increased gain that can serve higher frequencies and improved phase progression technology. The latter of the two enables engineers to address angular coverage issues by shaping radiation patterns and steering antenna array beams toward a desired direction.
A monopole phased antenna array steering a beam.
As it turns out, phased array antennas are a good choice for achieving these goals and thus for 5G technologies. We also use this type of antenna for other applications, like radar and storm detection.

A solid-state phased array radar system.
To improve the design of phased array antennas, we can use Butler matrix feed networks. These beamforming networks save on cost by fabricating the circuit as microstrip lines and performing beam scanning without expensive active devices. As we’ll see next, efficiently designing such a circuit is possible with the Transmission Line interface in the RF Module.
Modeling a Passive Butler Matrix Beamforming Feed Network
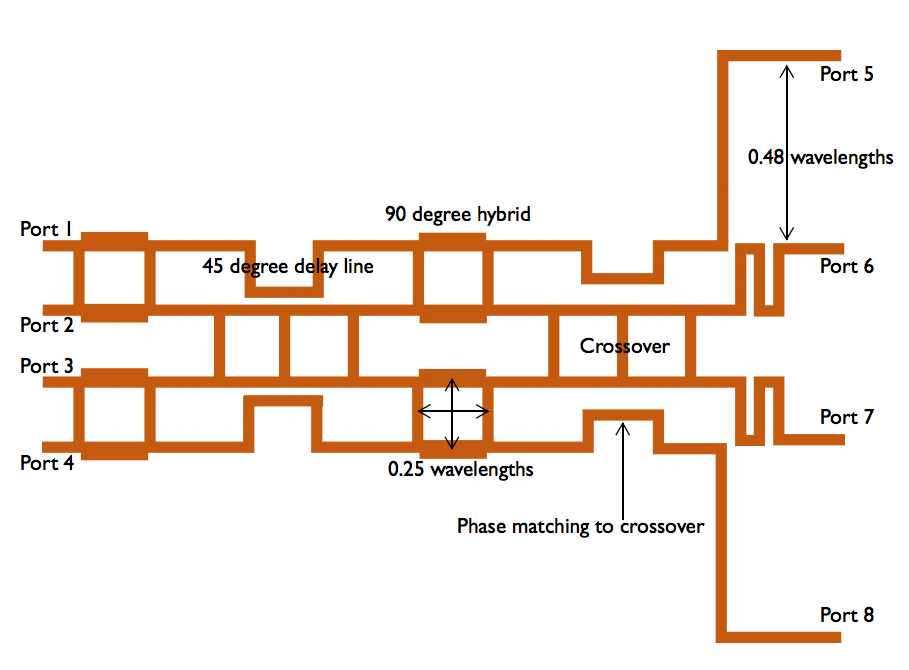
Before taking a look at our geometry as a whole, let’s discuss the individual subsections contained in this Butler matrix example.
These include:
- 90° hybrid coupler, such as a branch line coupler
- 45° delay lines
- Crossovers
- Transition parts that match the crossover and output phases
- Inner and outer front ends
These subsections repeat throughout the model, allowing us to simplify the geometry-building process by reusing each part as needed. All we have to do is add the subsections as geometry parts under the Global Definitions node.
Next, let’s examine a few of the individual subsections, starting with the 90° hybrid. This subsection consists of two output ports with a 90° phase difference and two input ports with no coupled power. The input power is equally divided into the output ports and due to the symmetric geometry, all input port configurations yield reciprocal circuit responses.
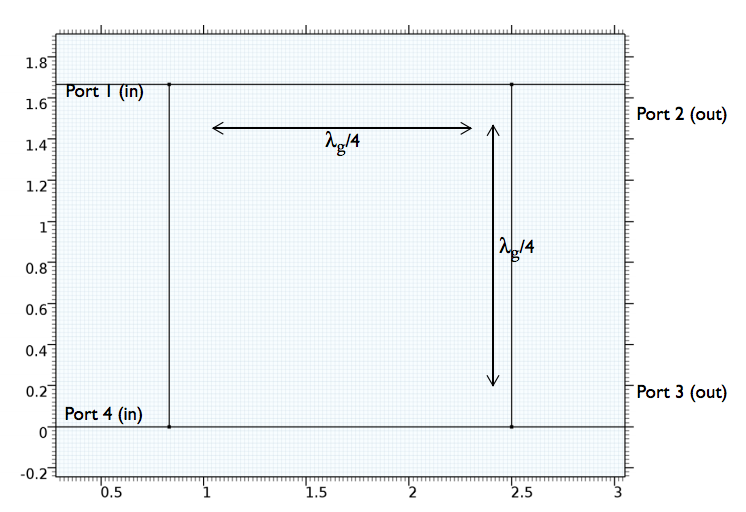
The geometry of a 90° hybrid coupler.
In the crossover structure, we use an even-odd analysis method to decouple the four-port network into two separate cascaded two-port networks that can be described with ABCD parameters. The resulting ladder-shaped crossover structure contains two isolated input ports that both produce input signals. These signals flow from inputs on the left side to outputs in the opposite corner, meaning that port 1 flows to port 3 while port 4 flows to port 2.
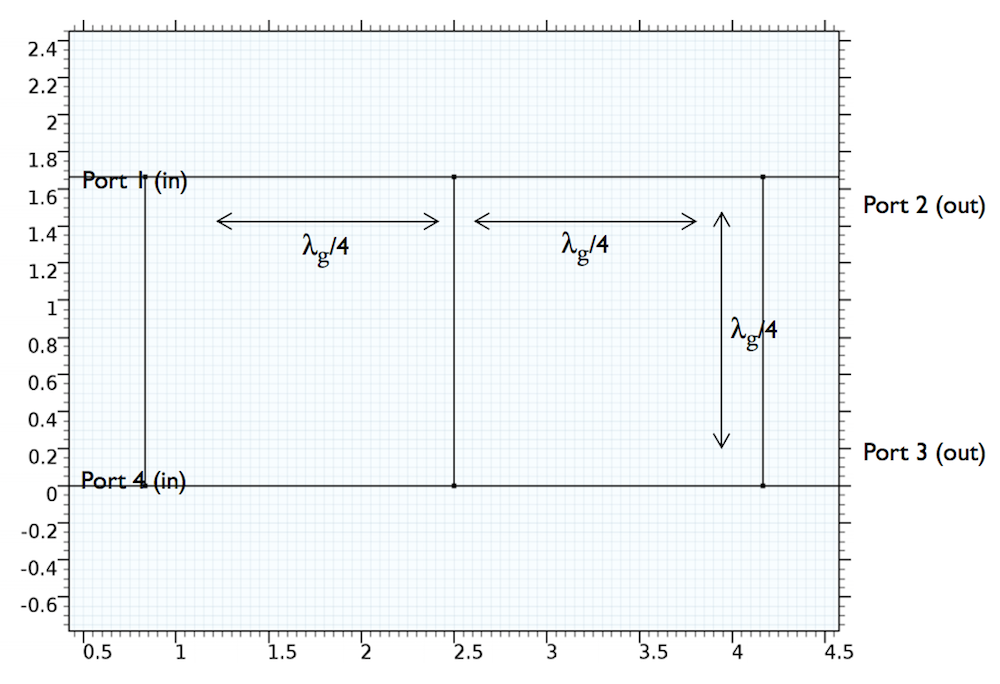
The geometry of the crossover structure. The port definitions seen here only relate to the subsection analysis.
The front-end parts enable us to avoid distorting the output phase relation when altering the distance between output ports. By increasing the distance between the antenna elements, we can achieve a higher gain for the antenna array. However, this also causes unwanted effects, like a grating lobe and higher sidelobe level. With this in mind, we choose an antenna array spacing configuration that results in a reasonable gain and sidelobe level.
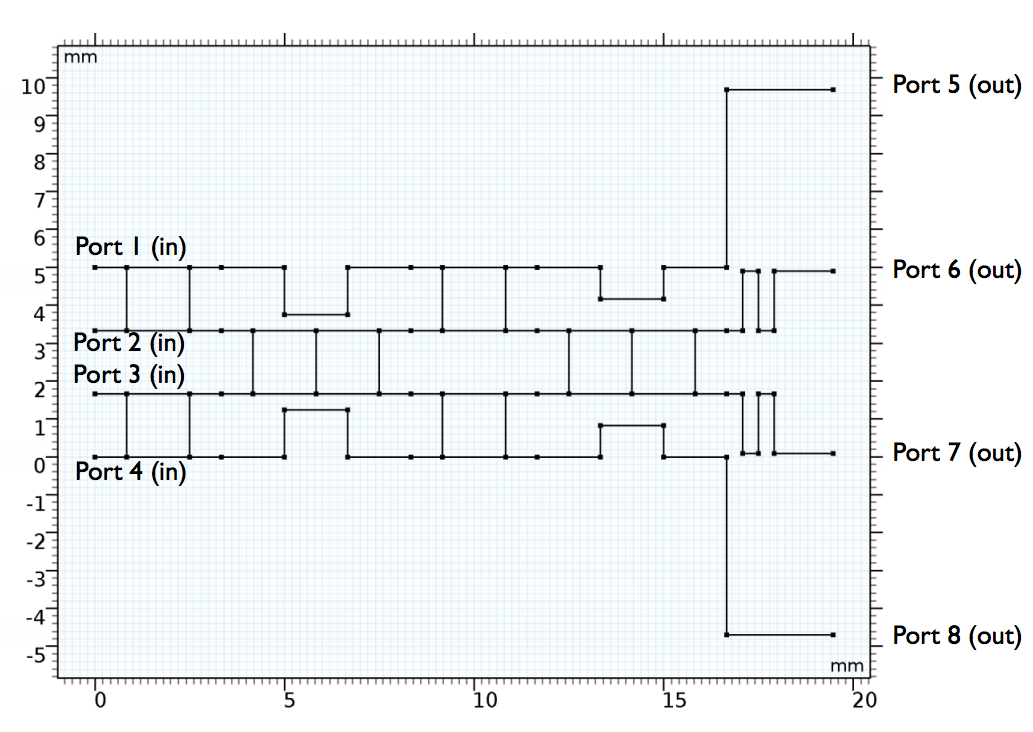
Putting all of this together, we create our Butler matrix beamforming network geometry, seen below. We use four 90° hybrids, two 45° delay lines, two crossovers, transition parts, inner front ends, and outer front ends.
A Butler matrix beamforming network schematic (left) and final geometry (right).
In our example, almost all of the distributed element parameters for the transmission lines can be placed on a 50-Ω microstrip line that is built onto a 20-mil lossless substrate and 1-oz copper without using any air bridges and by using holes.
Simulation Results
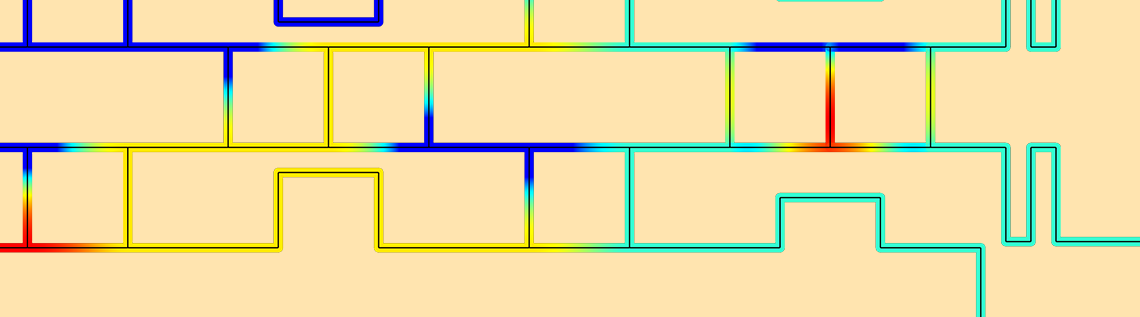
After running our simulation, we generate a default plot of the real voltage value on the transmission lines. By changing the default input expression, we create the logarithmic voltage value plot shown below. We see here that when port 4 is excited, ports 1–3 do not have coupled power and are isolated below -100 dB.
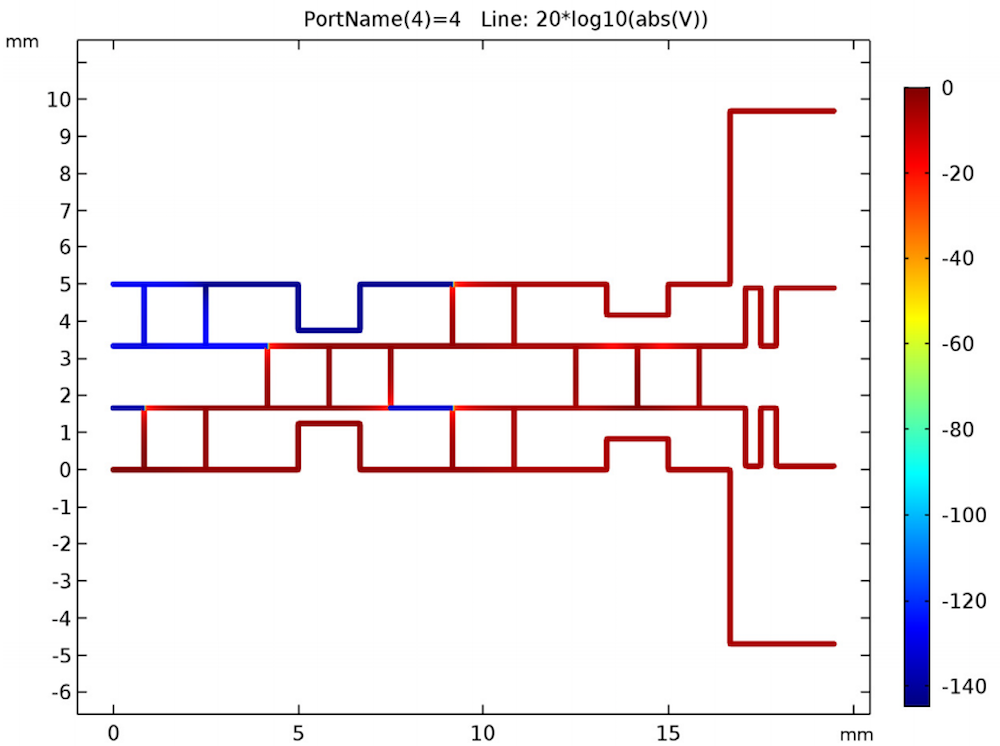
The dB-scaled voltage across the transmission lines when port 4 is excited.
To better examine the output port voltage levels, we can alter this plot by setting a minimum range of -10 dB. These results indicate that the input voltage is equally distributed to all of the output ports.
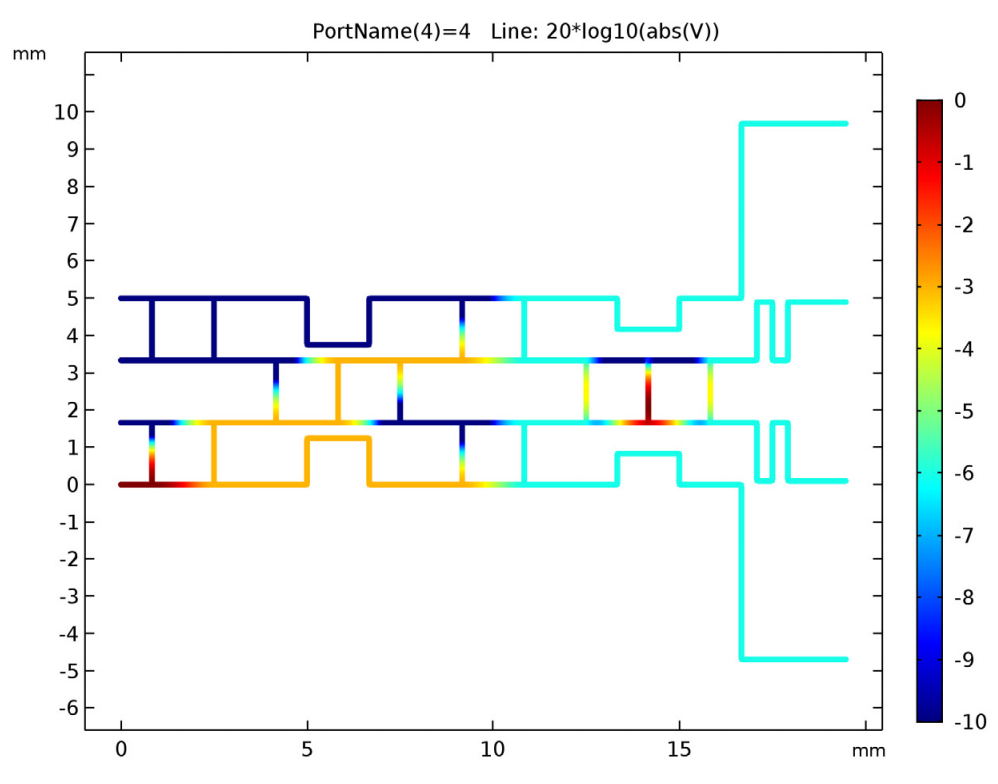
The dB-scaled voltage plot with an adjusted range.
We can also study the arithmetic phase progressions at the output ports. We easily configure the phase of each port in an arithmetic order by adjusting a few of the evaluated angles.
Using this technique, we excite the Butler matrix beamforming network with a 4-by-1 antenna array in the following order:
- Port 3 (-135°)
- Port 1 (-45°)
- Port 4 (45°)
- Port 2 (135°)
As a result, the antenna radiation pattern is steered from one side to another — a desired result for a phased array antenna.
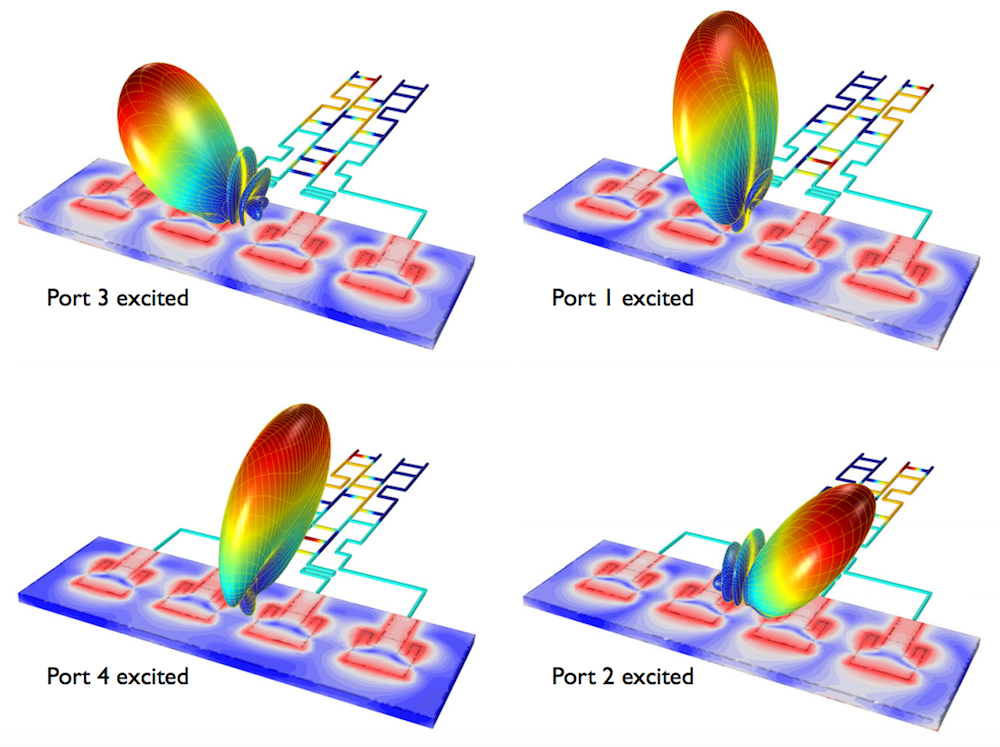
The far-field radiation pattern from a Butler matrix beamforming network connected to a 4-by-1 microstrip patch antenna array. Please note that this particular antenna array model is not part of the downloadable example.
Expanding the Results
These results can be extended to include different antenna arrays and Butler matrices. For example, in the animation below, the simulation is modified to include an 8-by-1 antenna array.
Steering antenna radiation pattern with an 8-by-1 antenna array connected to an 8-by-8 Butler matrix.
You might also be wondering if the Butler matrix can be deployed for a much larger system. The answer is of course! In the following designs, we simulate a 16-by-16 Butler matrix connected to an 8-by-1 microstrip patch antenna array and a 64-by-64 Butler matrix connected to an 8-by-8 microstrip patch antenna array.
Steering antenna radiation pattern with a 16-by-1 antenna array connected to a 16-by-16 Butler matrix.
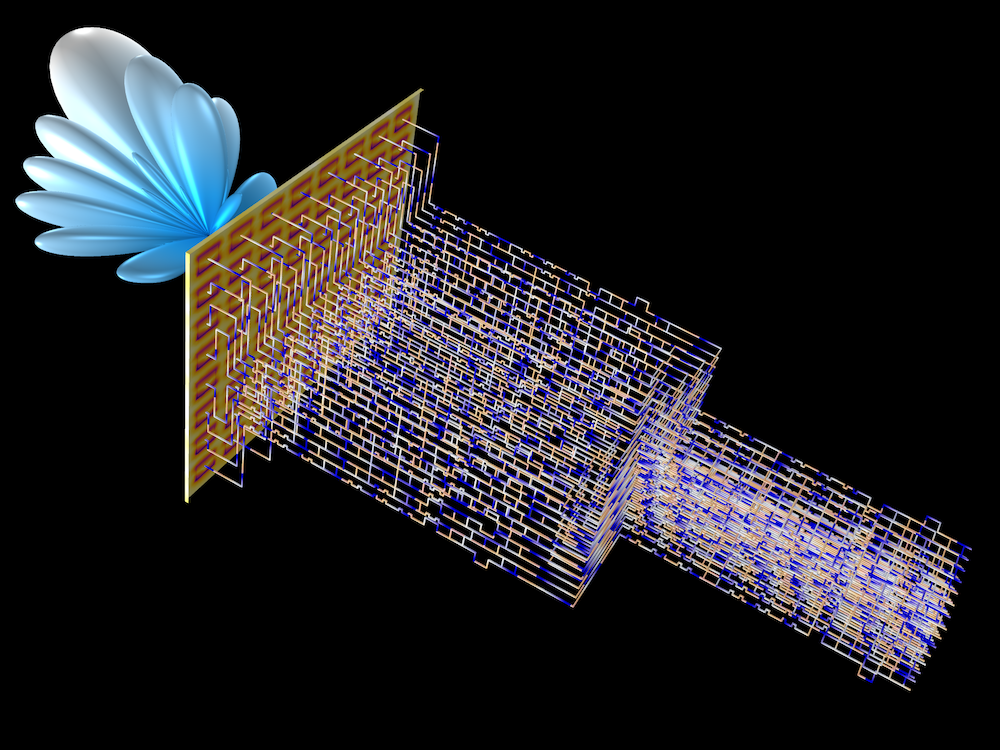
Steering antenna radiation pattern with an 8-by-8 antenna array connected to a 64-by-64 Butler matrix.
As we’ve seen today, COMSOL Multiphysics enables us to efficiently model and analyze Butler matrices. To try this example yourself, click on the button below and get the tutorial from the Application Gallery (note that it’s also available in the Application Library under RF_Module/Couplers_and_Power_Dividers/transmission_line_butler).






Comments (13)
Hailemichael Guadie
September 12, 2018how to connect or integrated Transmission Line Butler Matrix Beamforming Network and microstrip pach antenna???
Jiyoun Munn
September 12, 2018You can excite each microstrip patch antenna element with a lumped port where you may set the port voltage to the corresponding output of the Butler matrix, for example, tl.Vport_1.
michael Haile
October 4, 2018Caty Fairclough, please can you send me 8×8 transmission line butler matrix and 8×1 microstrip pach antenna final simulation or can tell me how to design it????
email. makehaile3@gmail.com
Brianne Costa
October 5, 2018Hi Michael,
You can access the MPH-files and tutorial documentation at the links below by logging into your COMSOL Access account and a valid software license):
https://www.comsol.com/model/transmission-line-butler-matrix-beamforming-network-42531
https://www.comsol.com/model/microstrip-patch-antenna-11742
michael Haile
October 12, 2018Hi, Brianne Costa, how are you ?/thanks you , your message or send me is 4×4 transmission line but i want 8×8 transmission and 8×1 microstrip antenna design
can you help me please ??
michael Haile
October 16, 2018i design 4×4 butler matrix but i want 8×8 butler matrix ,so how can expand 4×4 butler matrix to 8×8 butler matrix???????
Brianne Costa
October 16, 2018Hi Michael,
For further questions related to your model, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
michael Haile
October 19, 2018i need this one Brianne Costa, can you help me ?? 8×8 butler matrix
Michael Haile
November 6, 2018how can Transmission Line interface wit butler matrix ?????
who any one help me??
Michael Haile
November 6, 2018how can interface Transmission Line with butler matrix ?????
who any one help me??
violet columbus
August 4, 2020Does that mean that beam will form at same angle as is the phase difference when exciting a particular input port?
violet columbus
August 4, 2020Does that mean that beam will form at same angle as the phase difference incremented by input port?
MRUNAL DESHPANDE
February 27, 2021Hello Sir/Madam I have downloaded your 4×4 butler matrix 5.5 version,I m getting only the phase difference table.I want u to please guide me on how to proceed for getting S matrix,graph at particular frequency,radiation pattern graph,3D simulation of butler matrix(as seen in ur tutorial of 4×4 butler matrix),S-parameters graphs.Please do help me.Thanking you.